A large heavy box is sliding without friction down a smooth plane of inclination `theta.` From a point P on the bottom of the box, a particle is projected inside the box. The initial speed of the particle with respect to the box is u and the direction of projection makes an angle `alpha` with the bottom as shown in the figure:

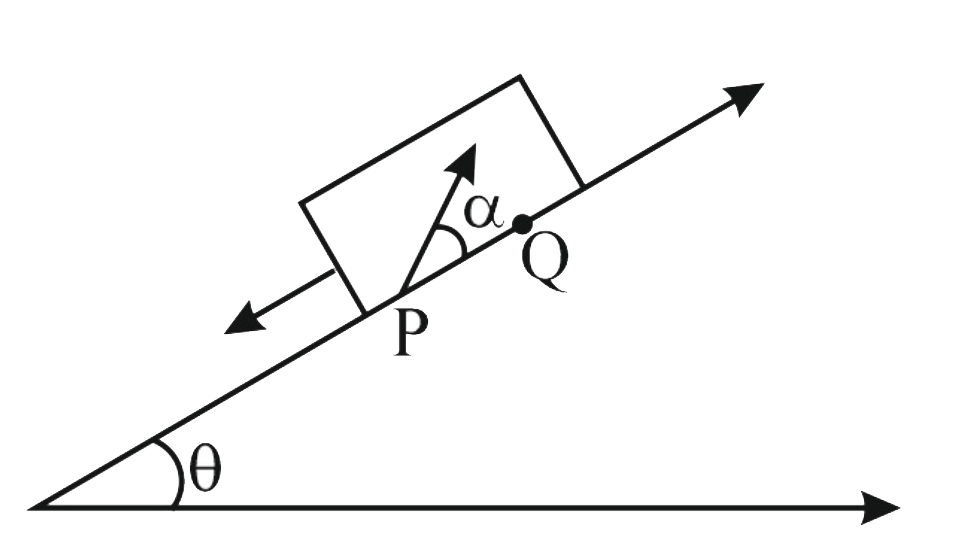
Find the distance along the bottom of the box between the point of projection P and the point Q where the particle lands.
[Assume that the particle does not hit any other surface of the box. Neglect air resistance]

Answer

(i) `(u^(2)sin 2alpha)/(g cos theta)` (ii) `v=(u cos (alpha+theta))/(cos theta)`

Explanation

(i) u is the relative velocity of the particle with respect to the box.

`u_(x)` is the relative velocity of particle with respect to the box in x-direction. `u_(y)` is the relative velocity with respect to the box in y-direction. Since there is no velocity of the box in the y-direction, therefore this is the vertical velocity of the particle with respect to ground also.
Y-direction motion
(Taking relative terms w.r.t. bx)
`u_(y)=+u sin alpha, a_(y)=-g cos theta`
`s=ut+1/2 at^(2)rArr 0=(u sin alpha)t-1/2 g cos theta xxt^(2)`
`rArr t=0` or `t=(2u sin alpha)/(g cos theta)`
X-direction motion
(taking relative terms w.r.t. box)
`u_(x)=+u cos alpha` & `s=ut+1/2 at^(2)`
`a_(x)=0 rArr s_(x)=u cos alphaxx(2u sin alpha)/(g cos theta)=(u^(2) sin 2alpha)/(g cos theta)`
(ii) for the observer (on ground) to see the horizontal displacement to be zero, the distance travelled by the box in time `((2u sin alpha)/(g cos theta))` should be equal to the range of the particle. Let the speed of the box at the time of projection of particle be u. Then for the motion of box with respect to ground.
`u_(x)=-v, s=vt+1/2 at^(@), a_(x)=-g sin theta`
`s_(x)=(-u^(2) sin 2alpha)/(g cos theta)=-c((2u sin alpha)/(g cos theta))-1/2 g sin theta ((2u sin alpha)/(g cos theta))^(2)`
On solving we get `v=(u cos (alpha+theta))/(cos theta)`