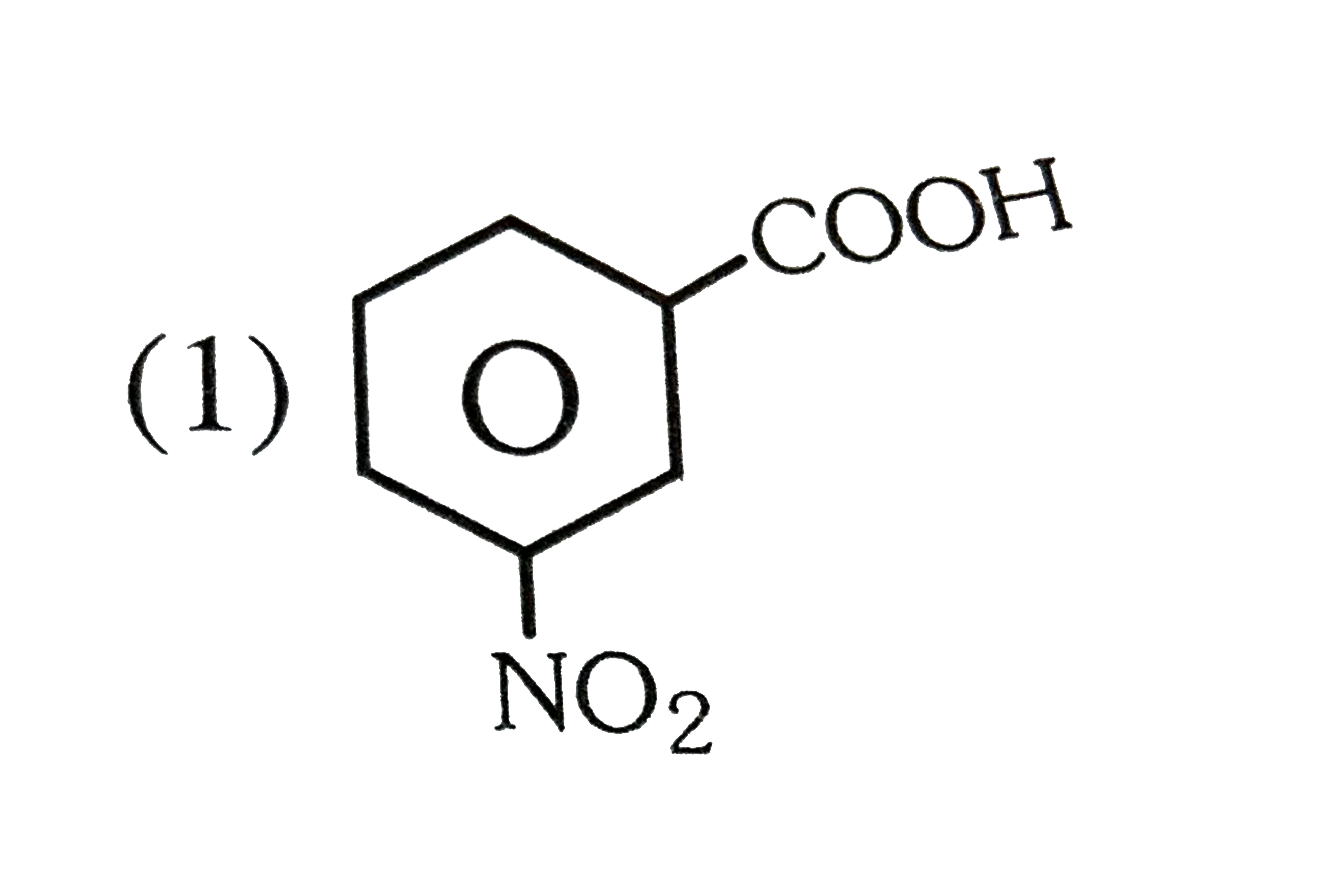
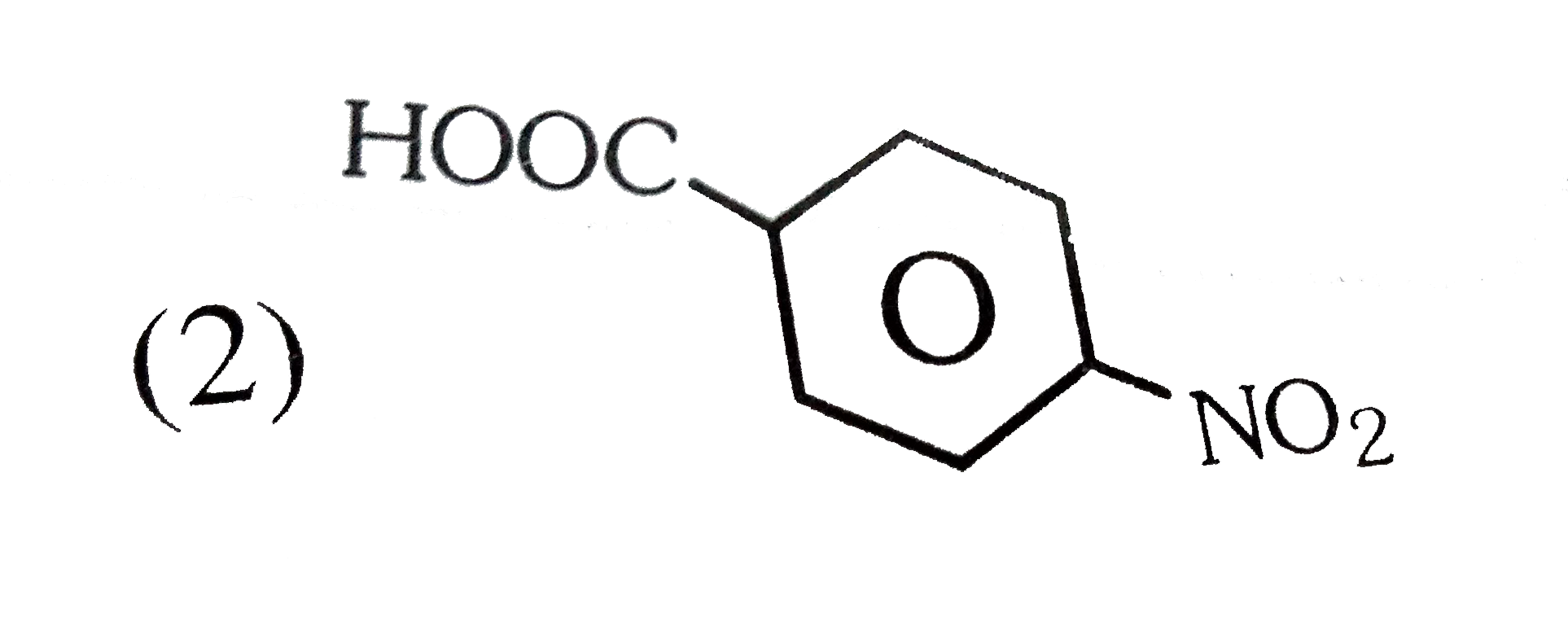
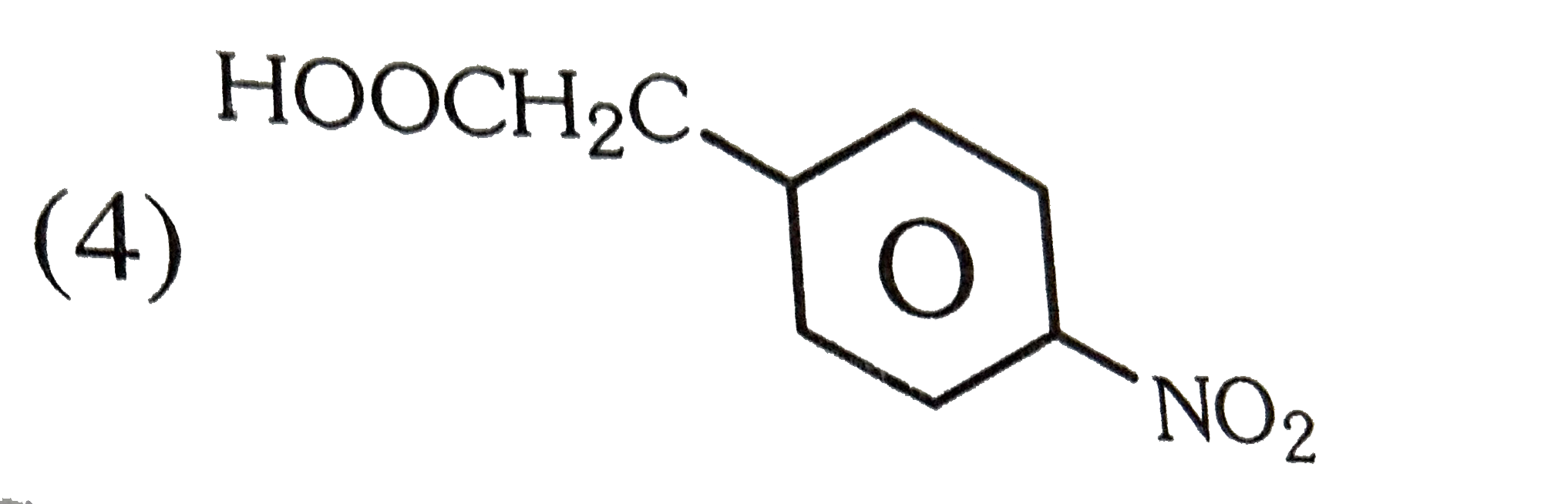
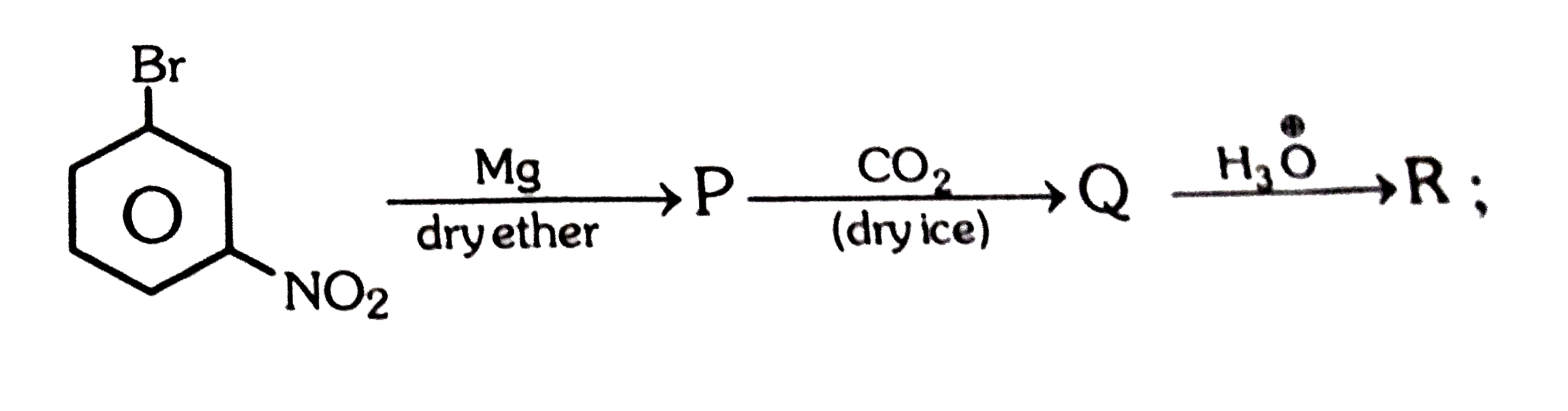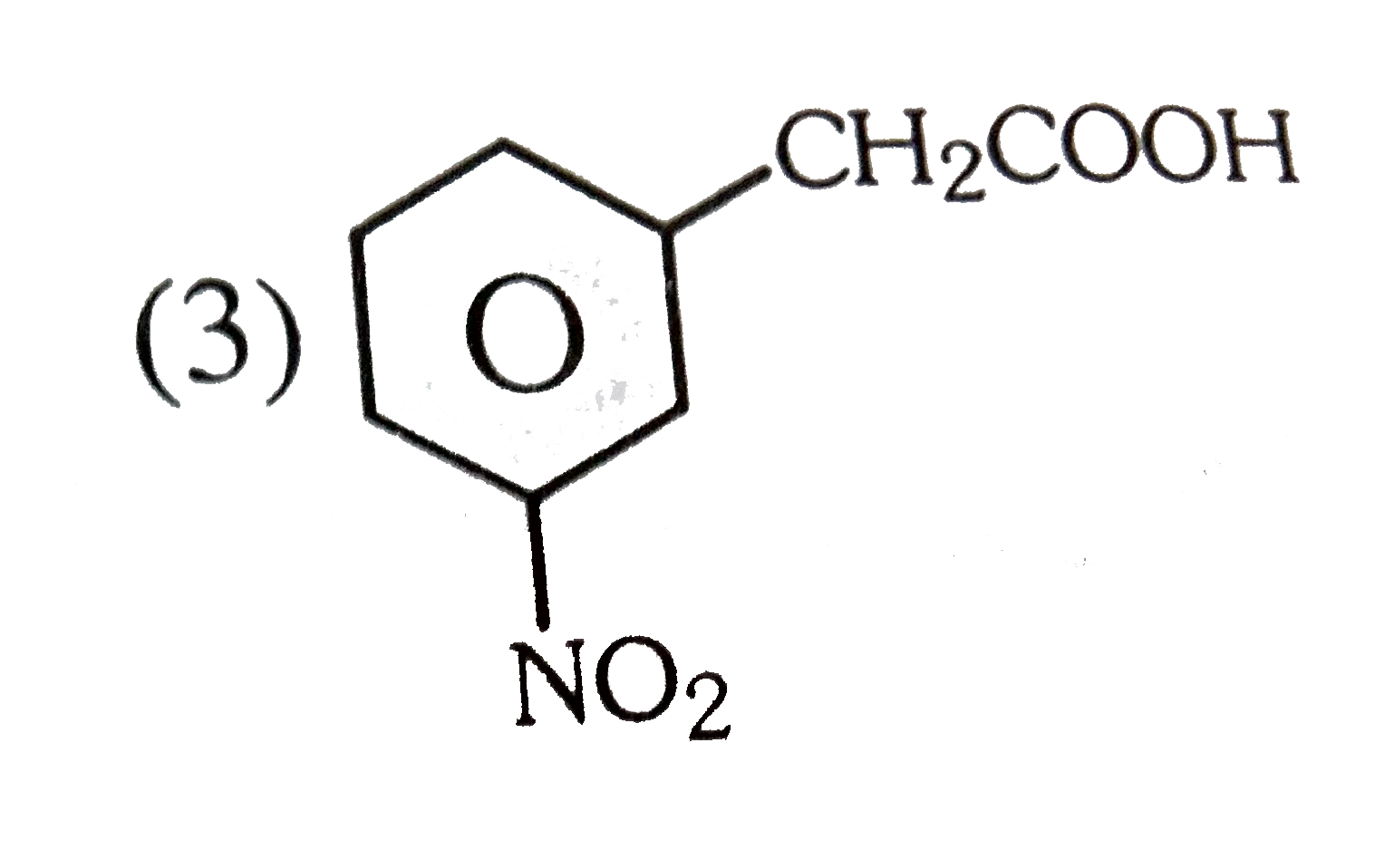A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-CHEMISTRY AT A GLANCE-ORGANIC CHEMISTRY
- Hydrolysis of which of the following gives acid at fastest rate :
Text Solution
|
- Complete the following reaction
Text Solution
|
- R is-
Text Solution
|
- H(3)C-COOHunderset(Delta)overset(P(2)O(5))(to)Aoverset(PCl(5))(to)Bund...
Text Solution
|
- Which of the following is not correctly matched
Text Solution
|
- Identify the end product : CH(3)CH(2)CH(2)CHOoverset(Ammonical AgNO(...
Text Solution
|
- Complete the following reaction
Text Solution
|
- What is Sandmeyer reaction ? Illustrate with a suitable example.
Text Solution
|
- Arrange the following compounds in increasing order of their boiling p...
Text Solution
|
- An amine reacts with C(6)H(5)SO(2)Cl and the product is soluble in alk...
Text Solution
|
- Which of the following compound cannot be formed by Gabriel phthalimid...
Text Solution
|
- Find out major product
Text Solution
|
- Product ( C) and (D ) will be:
Text Solution
|
- Product C and D are respectively:
Text Solution
|
- Which of the following conversion is incorrect :
Text Solution
|
- Which of the following compound gives yellow oily liquid nitrosamine w...
Text Solution
|
- Aniline can be obtained by : (a) C(6)H(5)COOHunderset(H^(o+))overse...
Text Solution
|
- Aniline cannot be obtained by :
Text Solution
|
- Aniline can be prepares by :
Text Solution
|
- Compound A is :
Text Solution
|