Home
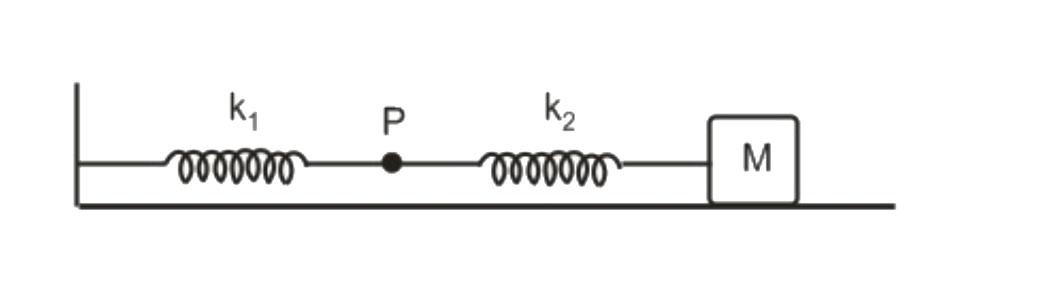
Class 12
PHYSICS
The mass M shown in figure ocillates in ...

The mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is

A

`(k_(1)A)/(k_(2))`

B

`(k_(2)A)/(k_(1))`

C

`(k_(1)A)/(k_(1) + k_(2))`

D

`(k_(2)A)/(k_(1) + k_(2))`

Text Solution

Verified by Experts

The correct Answer is:
D
In series force remain same, if extension in `k_(1)` and `k_(2)` are `x_(1)` and `x_(2)` respectively.
Then `k_(1)x_(1) = k_(2)x_(2)rArr x_(1)+x_(2) = A`
`rArr x_(1) + (k_(1)x_(1))/(k_(2)) = A rArr x_(1) (k_(1) + k_(2))/(k_(2)) = A`
`rArr x_(1) = (k_(2)A)/((k_(1) + k_(2)))`
Amplitude of point P will be the max, ext. in `k_(1)`.
So amplitude of point P is `(k_(2)A)/(k_(1)+k_(2))`
Promotional Banner

Topper's Solved these Questions

  • SIMPLE HARMONIC MOTION

    ALLEN|Exercise MCQ s one or more than one correct answers|5 Videos

  • SIMPLE HARMONIC MOTION

    ALLEN|Exercise Paragraph|3 Videos

  • SIMPLE HARMONIC MOTION

    ALLEN|Exercise Exercise-05 [A]|39 Videos

  • RACE

    ALLEN|Exercise Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)|24 Videos

  • TEST PAPER

    ALLEN|Exercise PHYSICS|4 Videos

Similar Questions

Explore conceptually related problems

A simple harmonic motino has amplitude A and time period T. The maxmum velocity will be

A particle oscillating in simple harmonic motion has amplitude 'a'. The distance from the mean position at which its velocity will be one half of the maximum velocity is

A particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is

The maximum velocity of a particle, excuting simple harmonic motion with an amplitude 7 mm , is 4.4 m//s The period of oscillation is.

A particle executing simple harmonic motion with an amplitude A. The distance travelled by the particle in one time period is

A particle executes simple harmonic motion with an amplitude of 10 cm. At what distance from the mean position are the kinetic and potential energies equal?

A particle is subjected to two simple harmonic motions of the same frequency and direction. The amplitude of the first motion is 4.0 cm and that of the second is 3.0 cm . Find the resultant amplitude if the phase difference between the two motion is (a) 0^(@) (b) 60^(@) ( c) 90 ^(@) (d) 180^(@)

An insect of negligible mass is sitting on a block of mass M, tied with a spring of force constant k. the block performs simple harmonic motion with amplitude A in front of a plane mirror placed as shown in the figure the maximum speed of insect relative to its image will be

An insect of negligible mass is sitting on a block of mass M, tied with a spring of force constant K. The block performs simple harmonic motion with amplitude A infront of a plane mirror placed as shown. The maximum speed of insect relative to its image will be

A pendulum is executing simple harmonic motion and its maximum kinetic energy is K_(1) . If the length of the pendulum is doubled and it perfoms simple harmonuc motion with the same amplitude as in the first case, its maximum kinetic energy is K_(2) Then: