A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-RACE-RACE 17
- Let x =(log(sin 30^(@))cos 30^(@))(log(cos30^(@))cot30^(@)) (log(cot 3...
Text Solution
|
- If tan^(4)theta +tan^(2) theta = 2, then the value of cos^(4)theta +co...
Text Solution
|
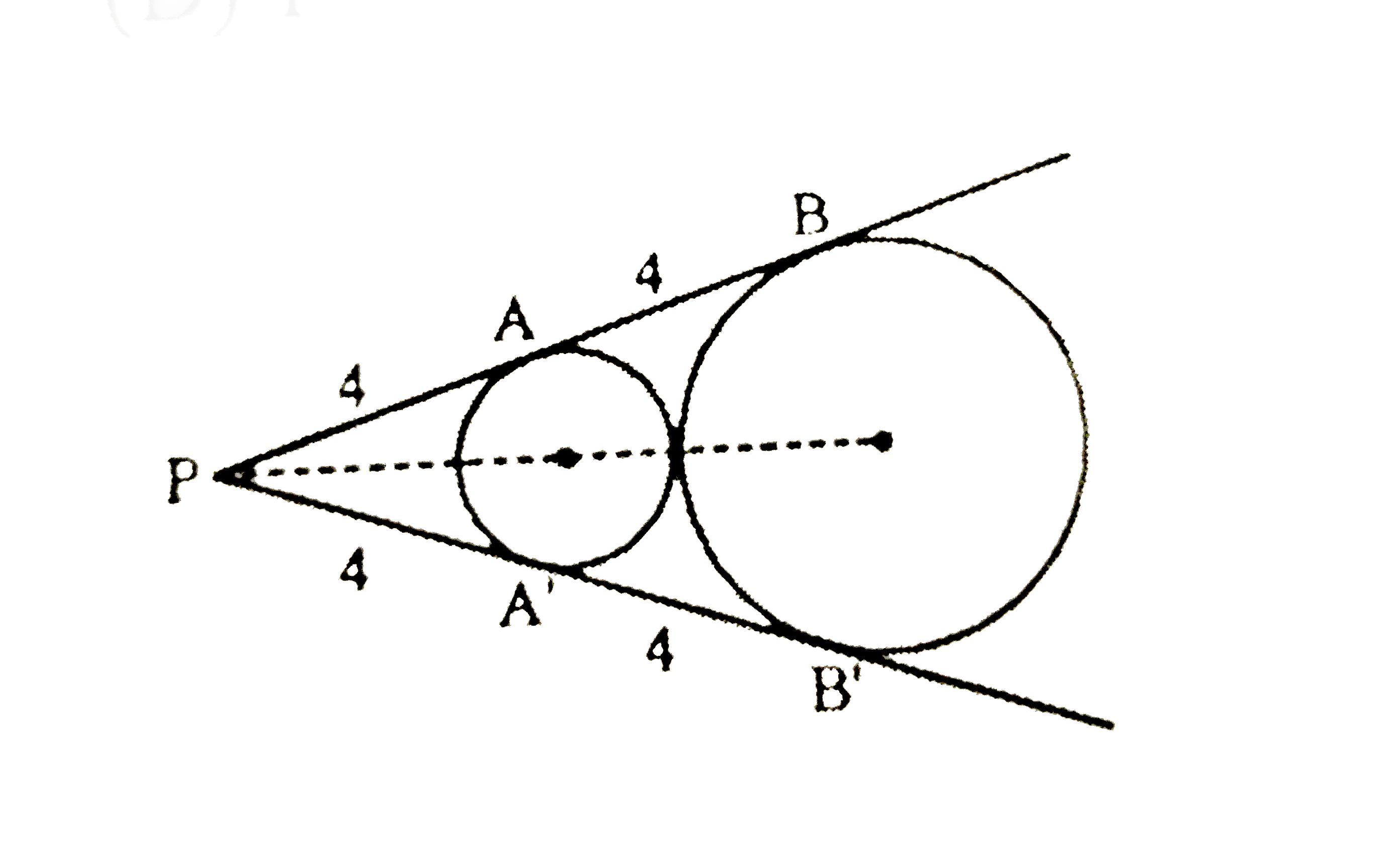
- Two circles are externally tangent. Lines PAB and PA'B' are common tan...
Text Solution
|
- Given that log(2) = 0.3010…., the number of digits in the number 200...
Text Solution
|
- If tan alpha and tan beta are two solutions of x^(2)-px +q = 0, cot al...
Text Solution
|
- The expression sqrt(sin^(4)(37.5)^(@)+4cos^(2)(37.5)^(@)) +sqrt(cos^(4...
Text Solution
|
- The number of solution (s) for the equation 2logxa+log(ax)a+3log(a^2x)...
Text Solution
|
- If x(1) and x(2) are the roots of the equation sqrt(2010)x^(log(2010^(...
Text Solution
|
- If the roots of x^(2)+ax +b = 0 are sec^(2)(pi)/(8) and coses^(2)(pi)/...
Text Solution
|
- {:(Column -I,Column -II),((A)"Anti logarithm of" (0.bar(6))"to the bas...
Text Solution
|
- Find the following integrals. 1. int 3x^(7)dx 2. int 4 sqrt(x)dx 3. ...
Text Solution
|
- A particle moves on x-axis as per equation x = (t^(3)- 9t^(2) +15+2)m....
Text Solution
|