Distance x of the body from the given fixed point and time t measured by the stopwatch are the suitable variables. If we consider the fixed point as the origin, distance x is known as the position coordinate of the body.
In the following figure it is shown that the body is no point A at the instant `t=0`and after a time t it reaches another point B covering a distance, which equals to product of speed and time interval. Thus, distance s covered by the body in time t is given by the following equation.
`s=2t`
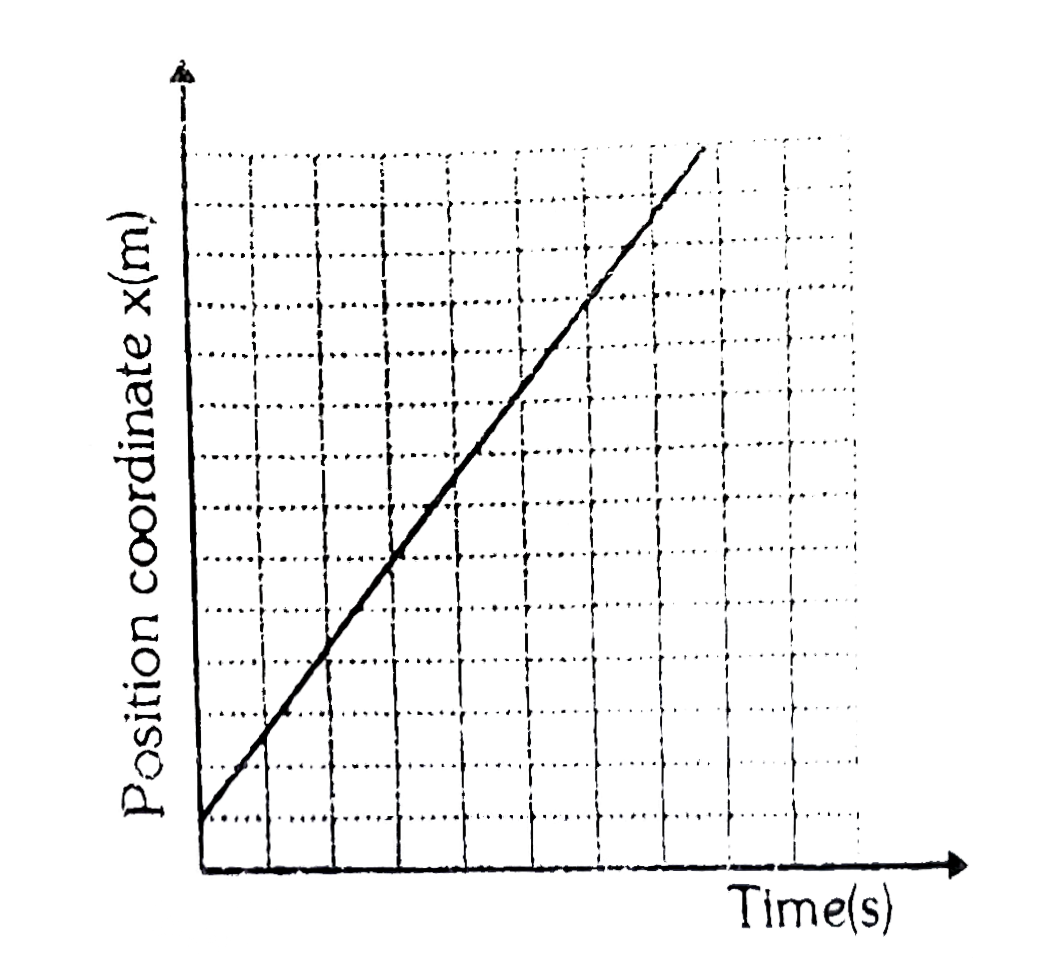
With the help of the above figure, position coordinate x of the body at any time t is given by the following equation, which is the required function describing motion of the body.
`x=2t+1`
Graph of this equation is also shown in the adjoining figure.