Home
Class 12
PHYSICS
If vecAxxvecB=vec0 and vecBxxvecC=vec0, ...

If `vecAxxvecB=vec0` and `vecBxxvecC=vec0`, then the angle between `vecA` and `vecC` may be:

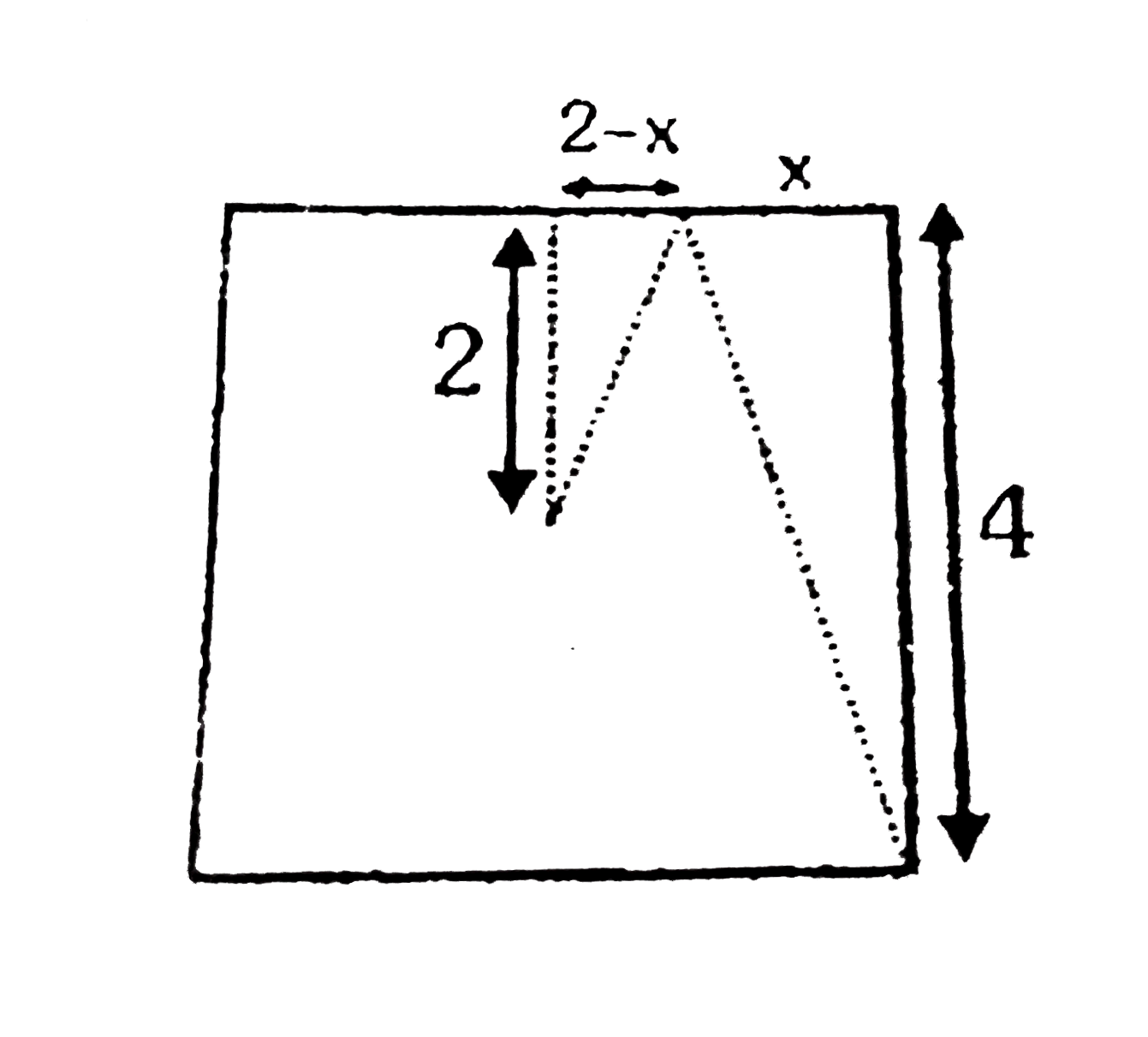
Text Solution

Verified by Experts

The correct Answer is:
`45^(@)`
`:' m=k tan theta`
`:. Dm= k sec^(2) theta d theta`
`rArr (dm)/m=(k sec^(2) theta)/(k tan theta) d theta`
`rArr (dm)/m=(d theta)/(sin theta cos theta)=(2d theta)/(sin 2theta)`
`rArr %` error is minimum when `sin 2 theta`
has maximum value hence `2theta=pi/2` or `theta=45^(@)`
Promotional Banner

Topper's Solved these Questions

Similar Questions

Explore conceptually related problems

If vec A cdot vec B =0 and vec A xx vec C=0 , then the angle between B and C is

If veca +vecb +vecc =vec0, |veca| =3 , |vecb|=5 and |vecc| =7 , then the angle between veca and vecb is

If |vecc|=2 , |veca|=|vecb|=1 and vecaxx(vecaxxvecc)+vecb=vec0 then the acute angle between veca and vecc is (A) pi/6 (B) pi/4 (C) pi/3 (D) (2pi)/3

Let veca, vecb and vecc be three having magnitude 1,1 and 2 respectively such that vecaxx(vecaxxvecc)+vecb=vec0 , then the acute angle between veca and vecc is

Let veca, vecb and vecc be three vectors having magnitudes 1,1 and 2 resectively. If vecaxx(vecaxxvecc)+vecb=vec0 then the acute angel between veca and vecc is

If |vec(a)+vec(b)|ge|vec(a)-vec(b)| then angle between vec(a) and vec(b) may be

If |vecaxxvecb|=1/sqrt3|veca.vecb| , find the angle between vec a and vecb

If three unit vectors veca, vecb and vecc " satisfy" veca+vecb+vecc= vec0 . Then find the angle between veca and vecb .

If veca and vecb are unit vectors such that (veca +vecb). (2veca + 3vecb)xx(3veca - 2vecb)=vec0 then angle between veca and vecb is

veca+vecb+vecc=vec0, |veca|=3, |vecb|=5,|vecc|=9 ,find the angle between veca and vecc .