A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Six resistance each of value r=5 Omega are connected between points A,...
Text Solution
|
- The value of (b-c)/(r(1))+(c-a)/(r(2))+(a-b)/(r(3)) is equal to
Text Solution
|
- For infinite ladder network containing identical resistance of R Omega...
Text Solution
|
- Four identical resistance are joined as shown in fig. the equivalent r...
Text Solution
|
- Four resistors R(1),R(2),R(3) and R(4) are connected between two termi...
Text Solution
|
- In the circuit shown in the fig the equivalent resistance between a an...
Text Solution
|
- Six resistance each of value r=5 Omega are connected between points A,...
Text Solution
|
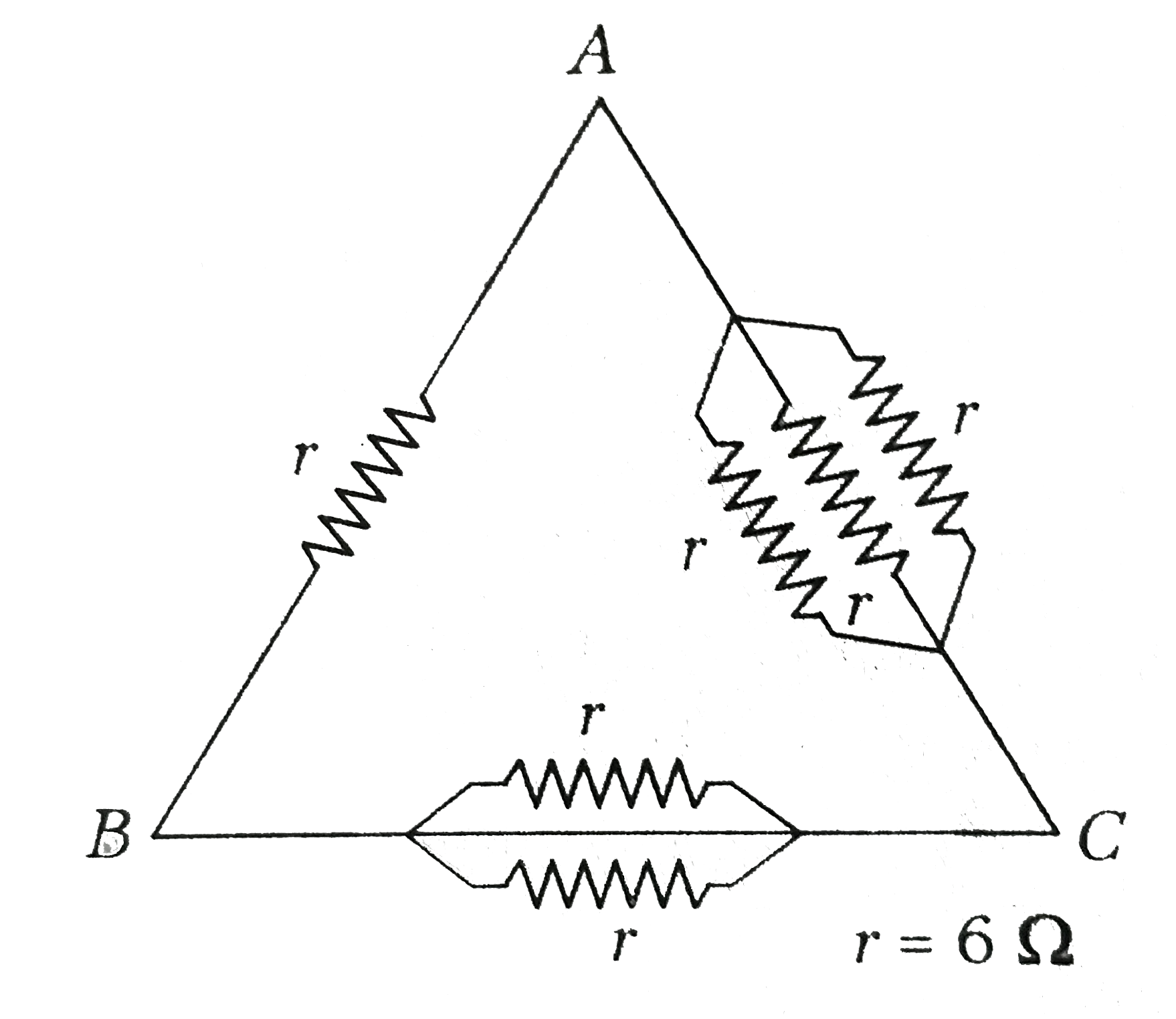
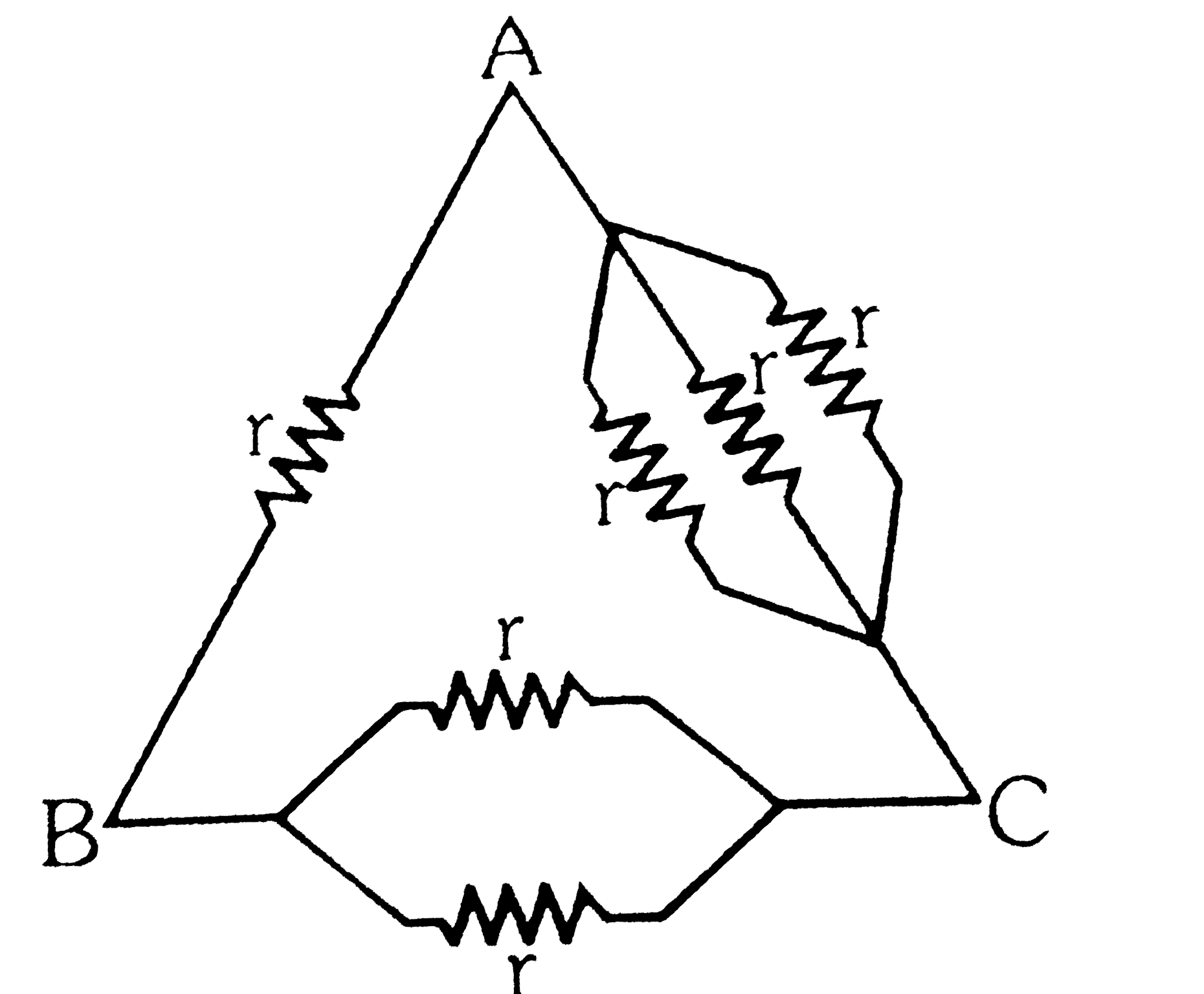
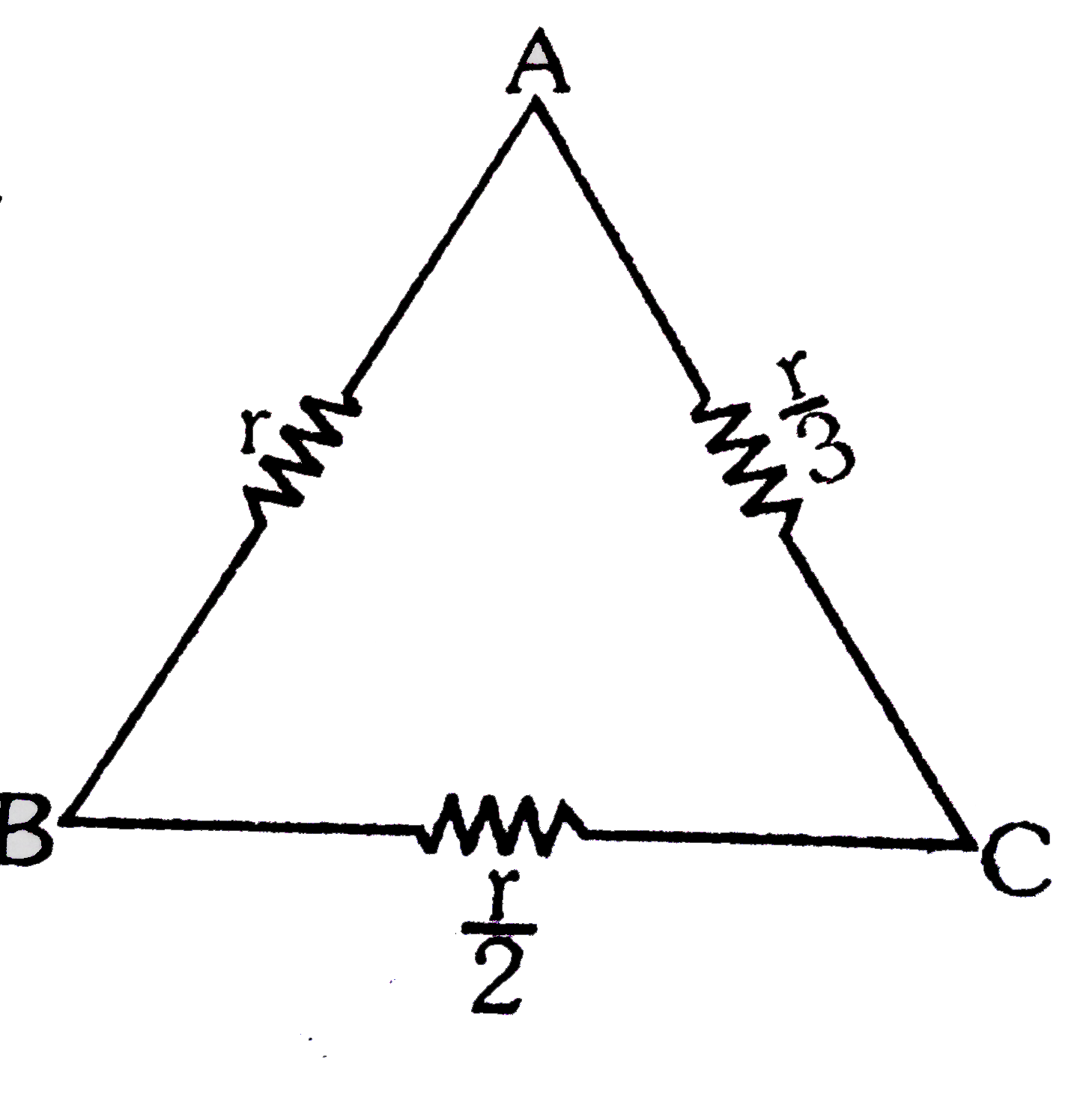
- Six resistances each of v ale r= 6Omega are connected between points A...
Text Solution
|
- value of the expression (b-c)/(r(1))+(c-a)/r(2)+(a-b)/r(3) is equal to
Text Solution
|