A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
RACE
ALLEN|Exercise Basic Maths (Thermal Physics) (Calorimetry)|14 VideosRACE
ALLEN|Exercise Basic Maths (Thermal Physics) (Mode of Heat Transfer)|14 VideosRACE
ALLEN|Exercise Basic Maths (Properties of Matter & Fluid Mechanics)(Surface Tension)|26 VideosNEWTONS LAWS OF MOTION
ALLEN|Exercise EXERCISE-III|28 VideosSIMPLE HARMONIC MOTION
ALLEN|Exercise Example|1 Videos
Similar Questions
Explore conceptually related problems
ALLEN-RACE-Basic Maths (Thermal Physics) (Temperature scales & thermal expansion)
- A circular metallic disc of radius R has a small circular cavity of ra...
Text Solution
|
- Two holes of unequal diameters d(1) and d(2)(d(1) gt d(2)) are cut in ...
Text Solution
|
- A beaker is completely filled with water at 4^(@)C. It will overflow i...
Text Solution
|
- Bars of two different metals are bolted together , as shown in figure....
Text Solution
|
- A thin wire of length l when heated to a certain temperature increases...
Text Solution
|
- On an X temperature scale, water freezing at -125.0^(@)C X and boils a...
Text Solution
|
- A glass thermometer is unmarked and has length of colum L(100^(@))=60 ...
Text Solution
|
- Two thermometers 'X' & 'Y' shows boiling point & freezing point of wat...
Text Solution
|
- The graph between two temperature scales A and B is shown in figure....
Text Solution
|
- Length v/s Temperature graph of A & B is given below. Find the relatio...
Text Solution
|
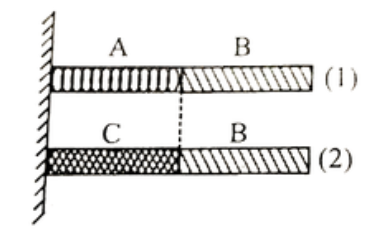
- Two composite rods made by A & B and C & B materials as shown. When we...
Text Solution
|
- A liquid with coefficient of volume expansion gamma is filled in a con...
Text Solution
|
- The apparent coefficient of expansion of a liquid when heated in a cop...
Text Solution
|