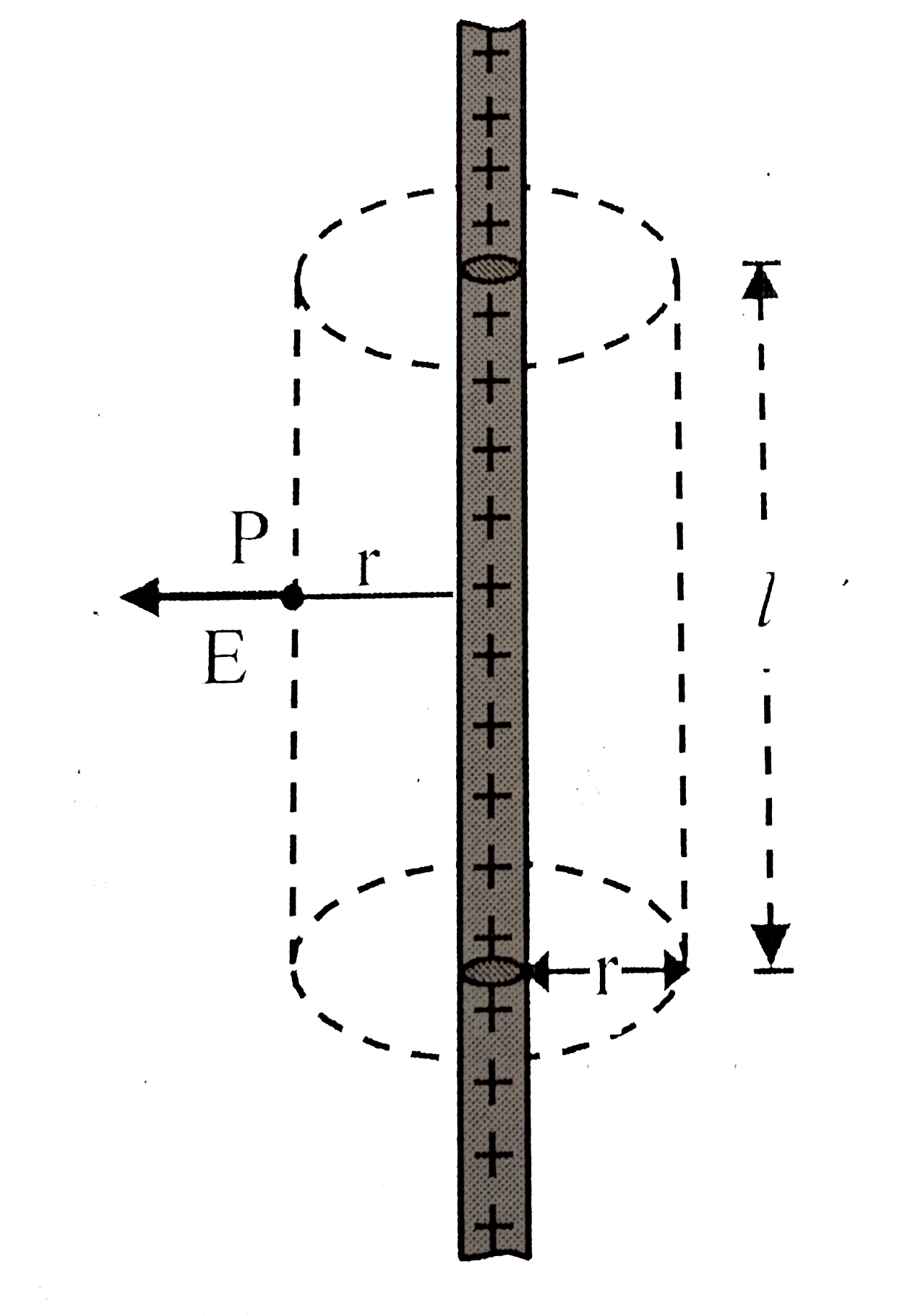Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ALLEN-TEST PAPER 1-PHYSICS
- The electric field lines coming out of an equipotential surface
Text Solution
|
- When unpolarised light is incident on the interface separating the rar...
Text Solution
|
- For the same angle of incidence, the angles of refraction in three dif...
Text Solution
|
- Write the necessary conditions for the phenomenon of total internal re...
Text Solution
|
- Answer the following, giving reason:- (a) When light travels from ...
Text Solution
|
- Prove that Refractive index=("real depth")/("apparent depth")
Text Solution
|
- Five point charges, each of value +q coulomb, are placed on five verti...
Text Solution
|
- The figure shows a modified Young’s double slit experimental set-up. H...
Text Solution
|
- A small ink dot on a paper is viewed through a glass slab of thickness...
Text Solution
|
- Using Gauss’ law, derive an expression for the electric field at a poi...
Text Solution
|
- (a) Derive the relation a sin theta=lambda for the first minimum of t...
Text Solution
|