A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
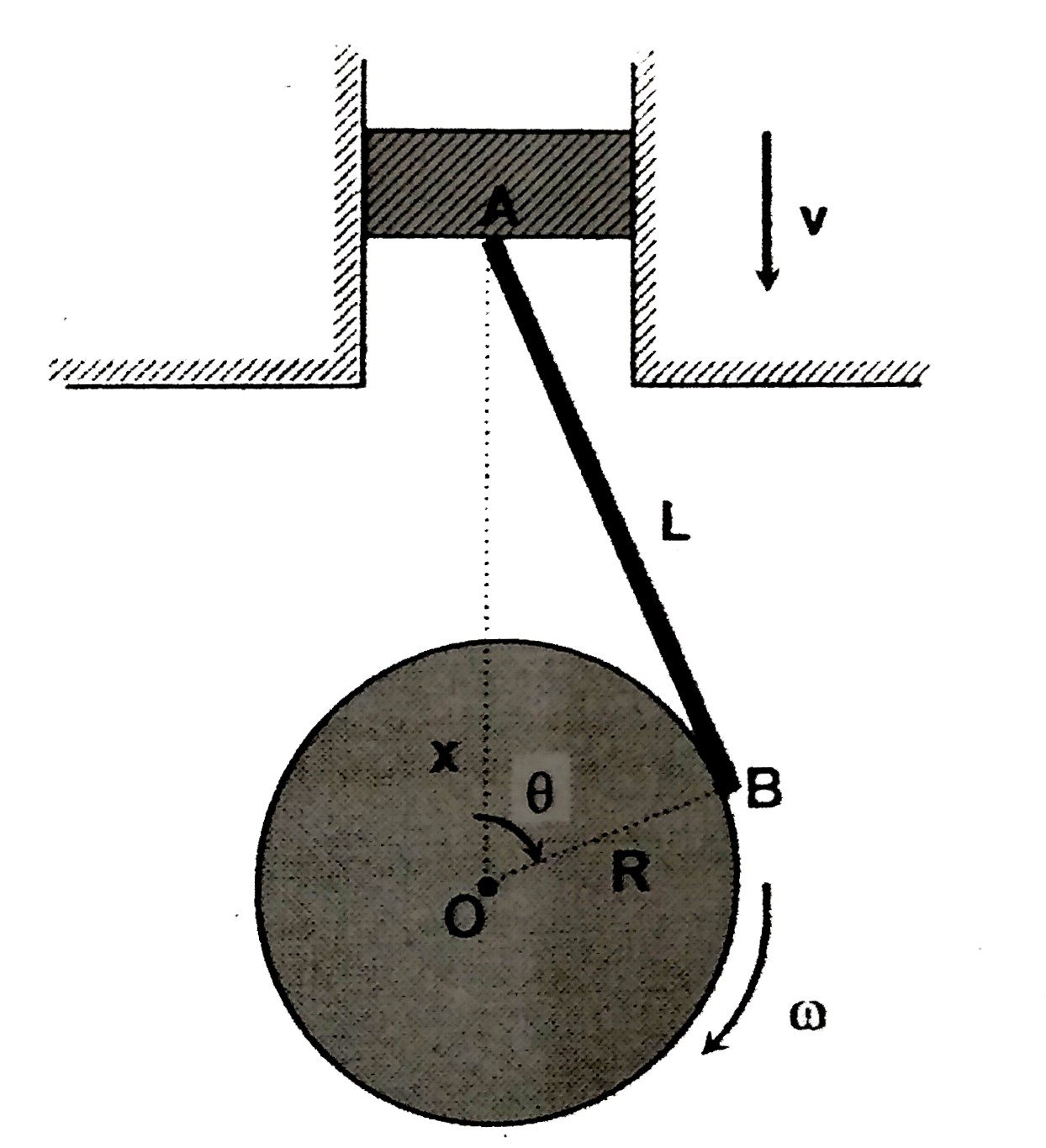
- Find velocity of piston A in the given situation if angular velocity o...
Text Solution
|
- A disc of radius R has linear velocity v and angular velocity omega as...
Text Solution
|
- A particle is moving with constant speed in a circle as shown in (Fig....
Text Solution
|
- A particle A moves along a circle of radius R=50cm so that its radius ...
Text Solution
|
- A particle 'A' moves along a circle of radius R = 50 cm, so that its r...
Text Solution
|
- One end of a rod of length L is fixed to a point on the circumference ...
Text Solution
|
- A thin circular ring of mass M and radius R is rotating about its axis...
Text Solution
|
- कोणीय वेग (omega) त्रिज्या (r) और रेखीय वेग (v) में संबन्ध है-
Text Solution
|
- Ring is fixed on the horizontal surface and a rod starts rotatiing wit...
Text Solution
|