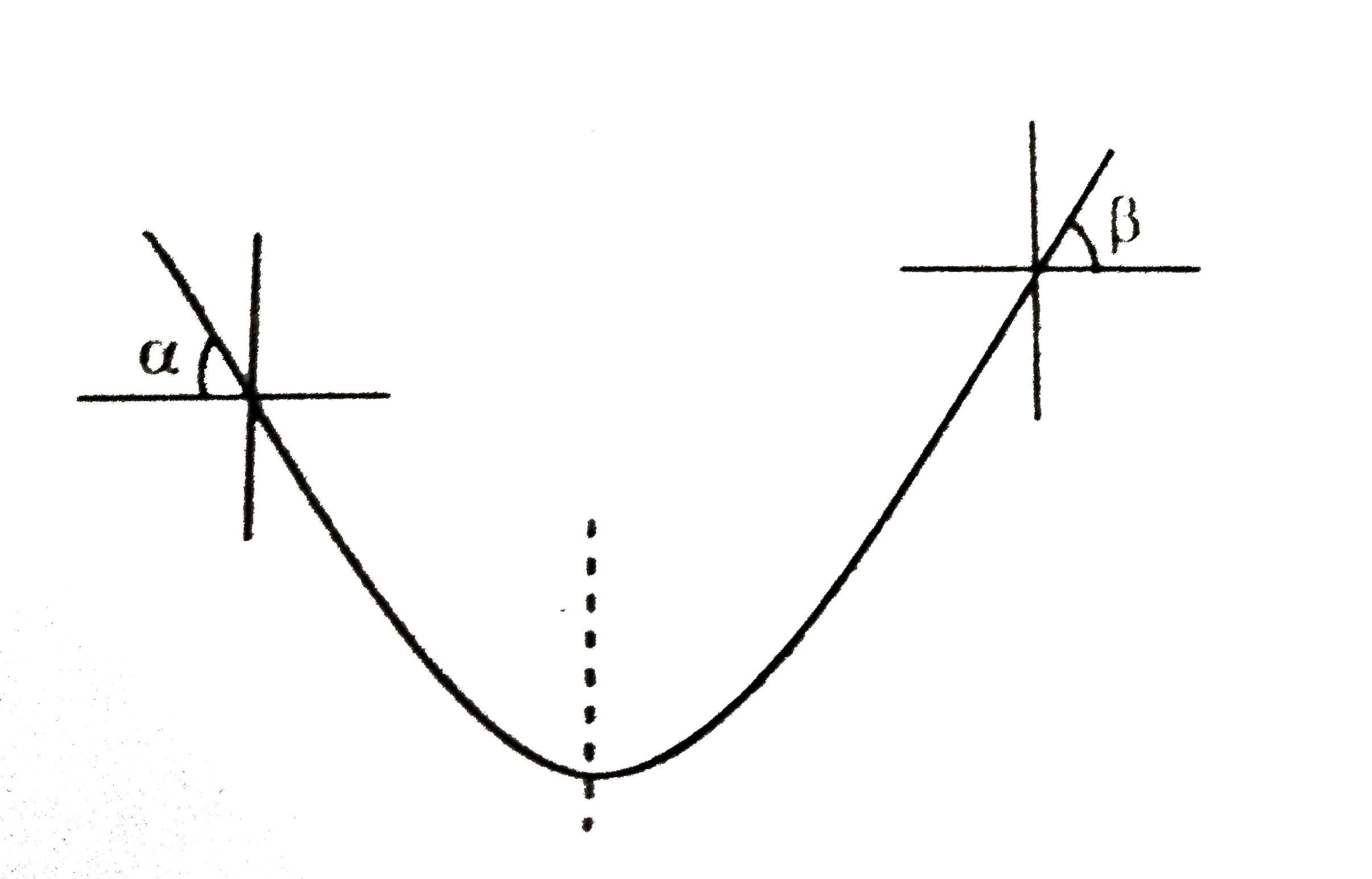
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- ltbrltgt A string of mass m (can be non uniform as well) is suspended ...
Text Solution
|
- Determine the tensions T(1) and T(2) in the string as shown in figure.
Text Solution
|
- A main revolves a stone of mass m tied to the end of a string in a cir...
Text Solution
|
- If tension in string A and string B are T(A) and T(B) then find out (T...
Text Solution
|
- A uniform rod of mass m and length L is suspended with two massless st...
Text Solution
|
- Determine the tension T(1) and T(2) in the strings shown in Fig.
Text Solution
|
- In fig tension in the string that connects the masses A and B is T(1) ...
Text Solution
|
- A system is at rest as shown in figure. The tension in the string in T...
Text Solution
|
- Determine the tension T(1) and T(2) in the strings
Text Solution
|
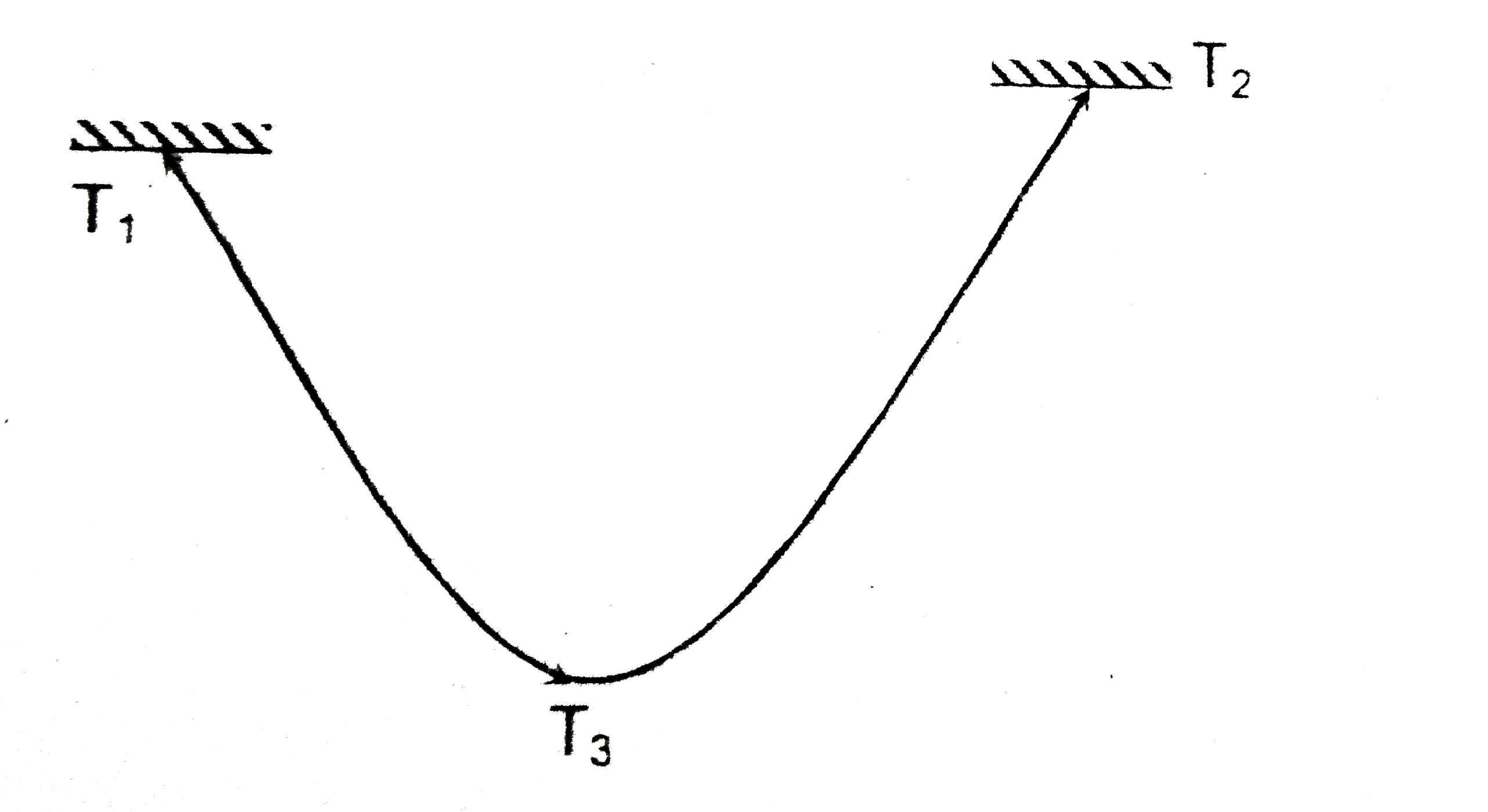 ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are `T_(1)` and `T_(2)` and at the lowest point is `T_(3)`. Mass of string in terms of `T_(1),T_(2)` and `T_(3)` can be represented a (uniform gravity 'g' exists downwards)
ltbrltgt A string of mass m (can be non uniform as well) is suspended through two points which are not in same horizontal level. Tension in the string at the end points are `T_(1)` and `T_(2)` and at the lowest point is `T_(3)`. Mass of string in terms of `T_(1),T_(2)` and `T_(3)` can be represented a (uniform gravity 'g' exists downwards)