Home
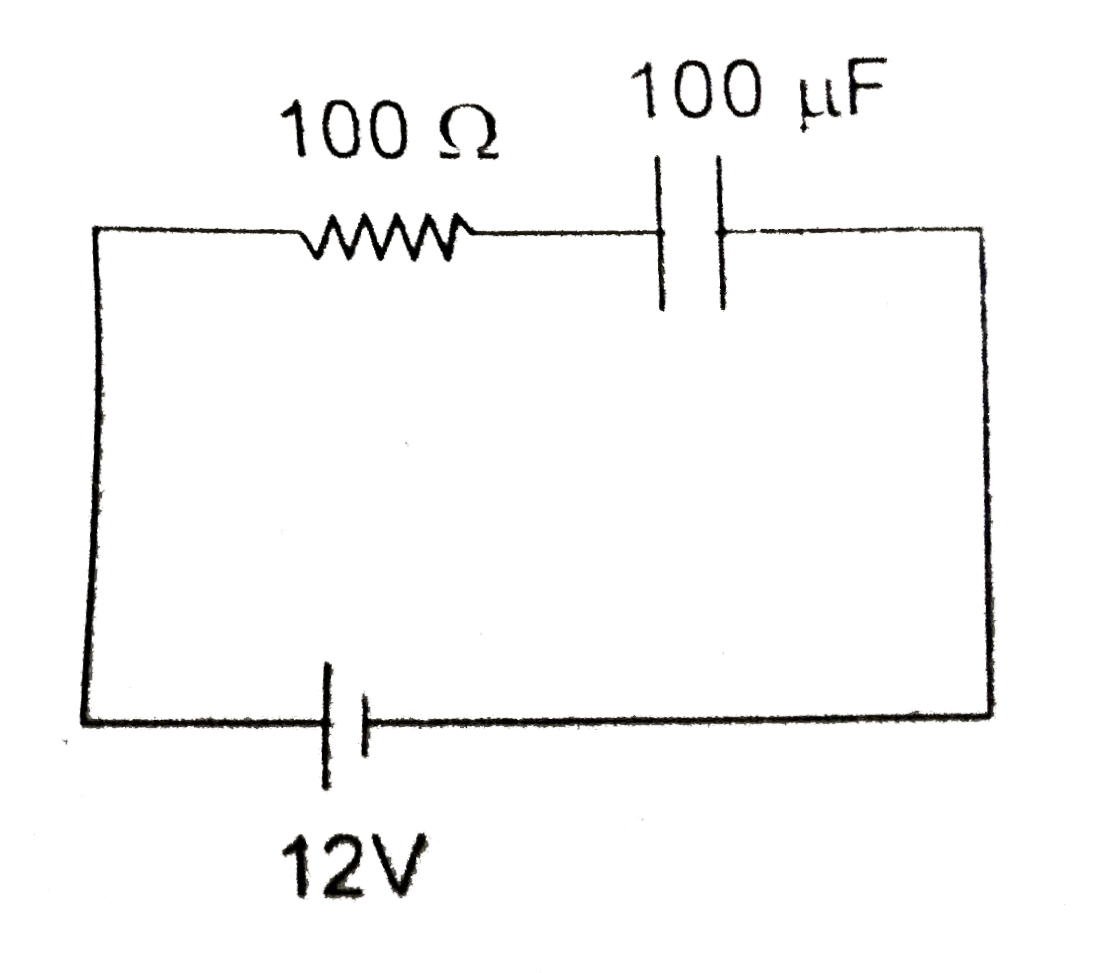
Class 12
PHYSICS
The value of displacement current at t=1...


The value of displacement current at `t=1` time constant is

A

`(120)/(e)`

B

`(120)/(e^(2))`

C

120 mA

D

none of these

Text Solution

Verified by Experts

The correct Answer is:
A
For continuity dispalcement current should be equal to conduction current
`q=q_(0)(1-e^(-t//RC))implies|i|=(q_(0))/(RC)e^(-t//RC)CR=t`
`implies(1200muF)/(ex1)impliesi=(0.0012)/(e)A=(1.2)/(e)mA`
Promotional Banner

Similar Questions

Explore conceptually related problems

A point mives in a straight line so its displacement x mertre at time t second is given by x^(2)=1+t^(2) . Its aceleration in ms^(-2) at time t second is .

Assertion : Displacement current goes through the gap between the plates of a capacitor when the charge of the capacitor does not charge Reason : The displacement current arises in the region in which the electric field is constant with time.

A : The displacement current goes through the gap between the plates of a capacitor when the charge on the capacitor does not change. R : Displacement current arises only when the electric field is constant.

The magnitude of displacement of a particle moving in a circle of radius a with constant angular speed omega varries with time t is

Assertion: Current versus time graph is as shown in figure, rms value of current is 4A. Reason: For a constant current, rms current is equal to that constant values. Reason: For a constant current, rms current is equal to that constant value.

Starting from rest a particle is first accelerated for time t_1 with constant acceleration a_1 and then stops in time t_2 with constant retardation a_2. Let v_1 be the average velocity in this case and s_1 the total displacement. In the second case it is accelerating for the same time t_1 with constant acceleration 2a_1 and come to rest with constant retardation a_2 in time t_3. If v_2 is the average velocity in this case and s_2 the total displacement, then

Starting from rest a particle is first accelerated for time t_1 with constant acceleration a_1 and then stops in time t_2 with constant retardation a_2. Let v_1 be the average velocity in this case and s_1 the total displacement. In the second case it is accelerating for the same time t_1 with constant acceleration 2a_1 and come to rest with constant retardation a_2 in time t_3. If v_2 is the average velocity in this case and s_2 the total displacement, then

A constant force acts on a particle and its displacement x (in cm) is related to the time t (in s) by the equation t=sqrtx +3 , when the velocity of the particle is zero, its displacement ( in cm) is

A body is moved from rest along a straight line by a machine delivering constant power. The ratio of displacement and velocity (s//v) varies with time t as

A body is moved from rest along a straight line by a machine delivering constant power. The ratio of displacement and velocity (s//v) varies with time t as