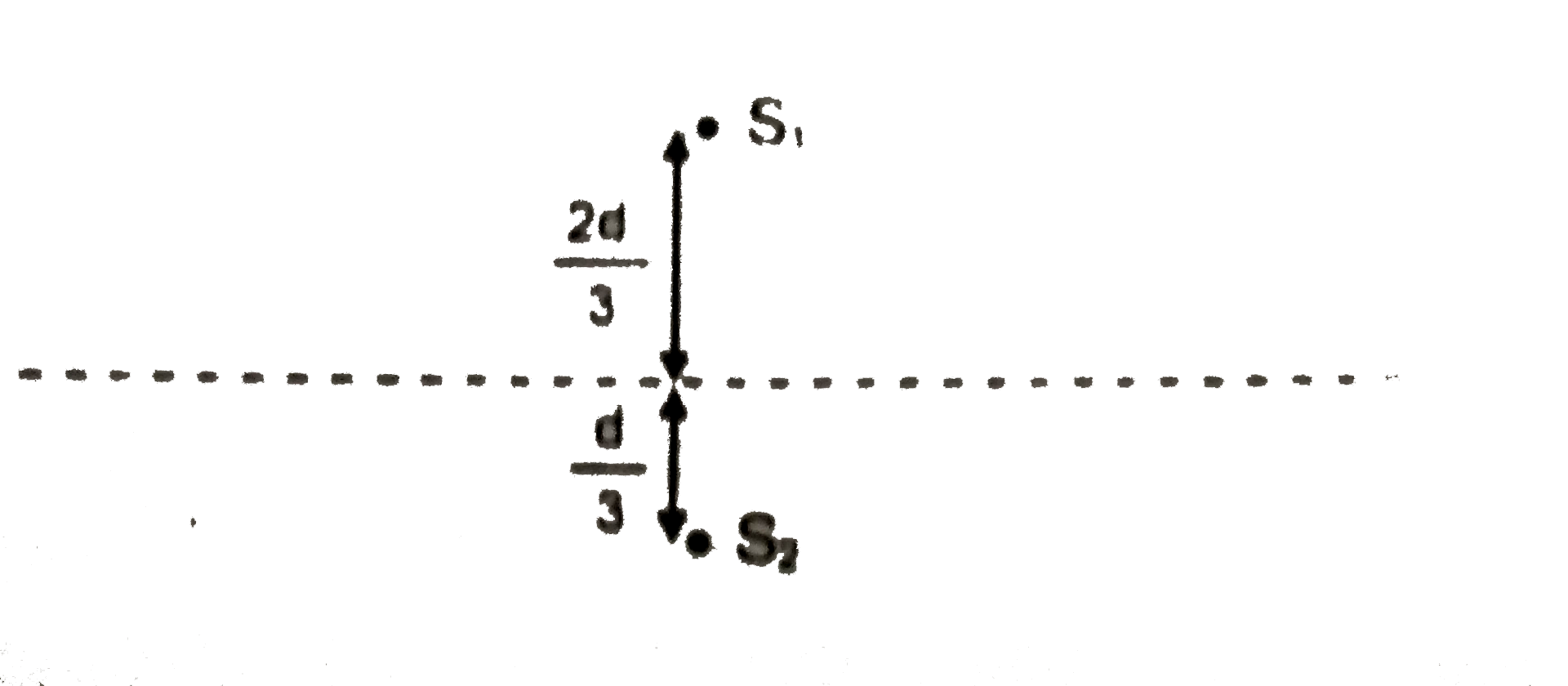
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two coherent point source of frequency (f=(10v)/(d) where v is speed o...
Text Solution
|
- A source of frequency f is moving towards the observer along the line ...
Text Solution
|
- Two points nonochromatic and coherent sources of light of wavelength l...
Text Solution
|
- A statinary observer receives a sound of frequency 2000 Hz. The variat...
Text Solution
|
- A source of sound of frequency 300 Hz and a receiver are located along...
Text Solution
|
- Two radius antennas radiating wave in phase are located at point A and...
Text Solution
|
- If two coherent source are placed at a distance 3lambda from each othe...
Text Solution
|
- A point source has been placed as shown in the figure-. What is the le...
Text Solution
|
- In YDSE apparatus shown in figure wavlength of light used is lambda. T...
Text Solution
|