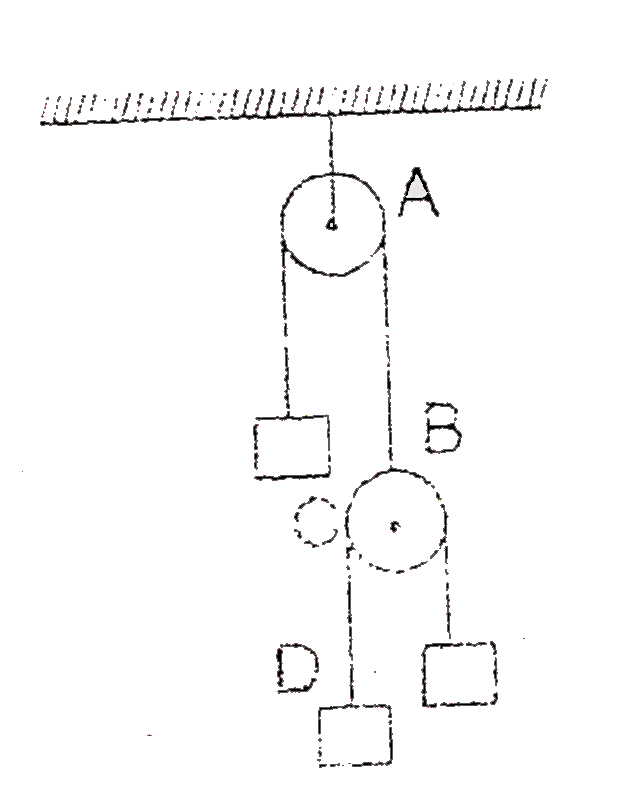A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Both the strings, shown in figure, are made of same material and have ...
Text Solution
|
- Both strings shown in figure, are made of same material and have same ...
Text Solution
|
- Two vibrating strings of the same material but lengths L and 2L have ...
Text Solution
|
- Both the strings shown in figure are mode of same material and have sa...
Text Solution
|
- both the strings , shown in figure are made of same material and have ...
Text Solution
|
- Both the strings, shown in figure, are made of same material and have ...
Text Solution
|
- Both the strings, shown in figure, are made of same material and have ...
Text Solution
|
- Two strings A and B, made of same material, are stretched by same tens...
Text Solution
|
- Both the strings, shown in figure, are made of same material and have ...
Text Solution
|