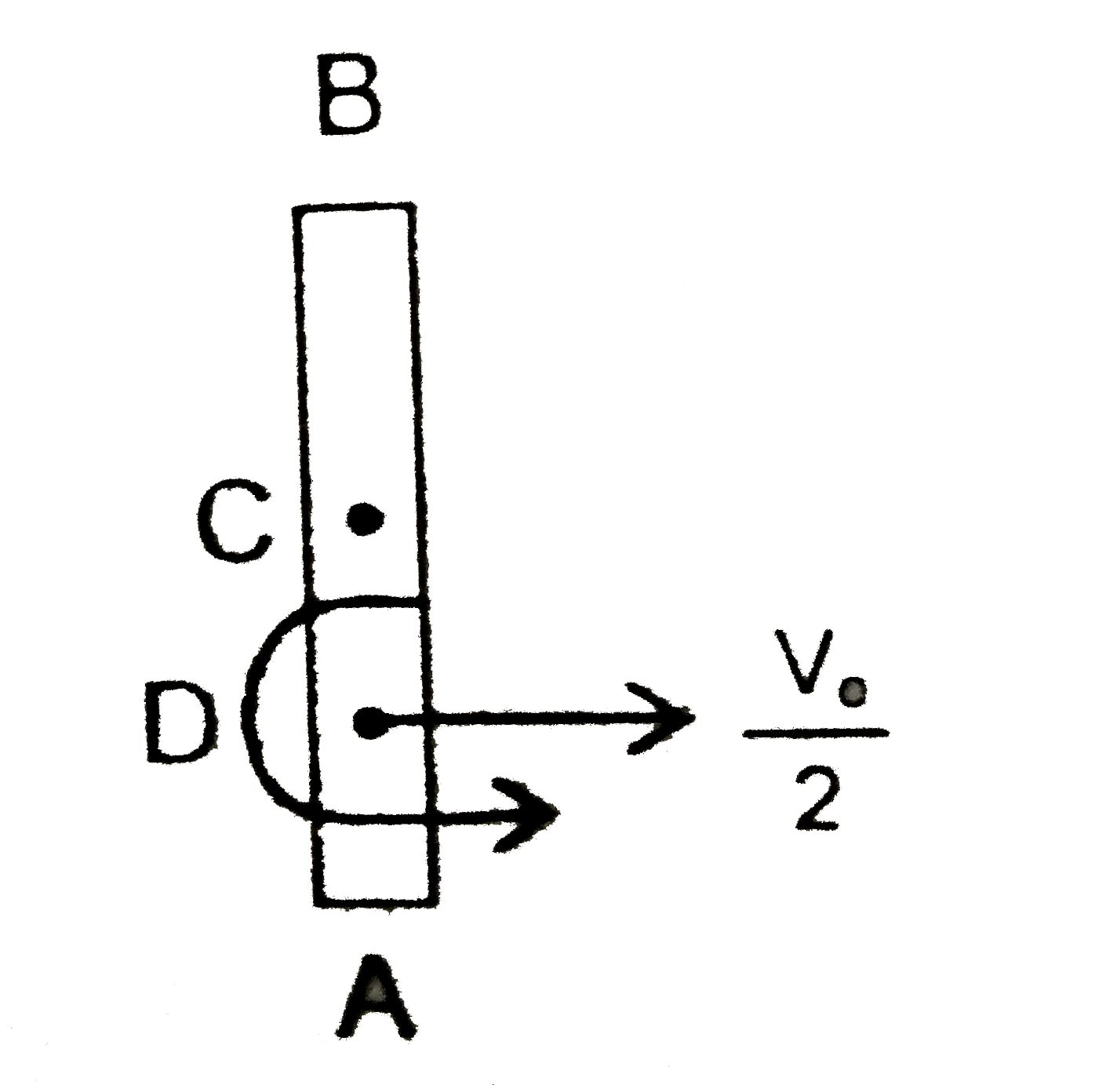
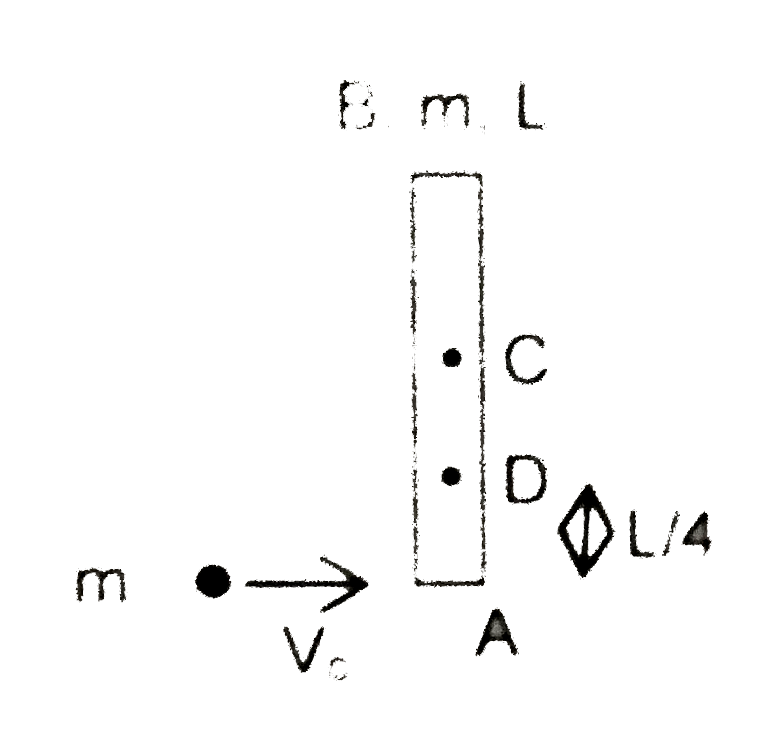A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A thin, uniform rod of mass M and length L is at rest on a smooth hori...
Text Solution
|
- A uniform rod of length l and mass 2 m rests on a smooth horizontal ta...
Text Solution
|
- A uniform rod of mass m , length l rests on a smooth horizontal surfac...
Text Solution
|
- A thin uniform rod of mass m and length l is kept on a smooth horizont...
Text Solution
|
- A uniform rod of length l and mass 2m rests on a smooth horizontal tab...
Text Solution
|
- A uniform rod of mass M and length L lies on a frictionless horizontal...
Text Solution
|
- A uniform rod of length l and mass 2m rests on a smooth horizontal tab...
Text Solution
|
- A uniform rod AB of mass m and length l is at rest on a smooth horizon...
Text Solution
|
- एक पतली छड़ का द्रव्यमान M तथा लम्बाई l है। छड़ के एक सिरे से l//3 दूरी ...
Text Solution
|