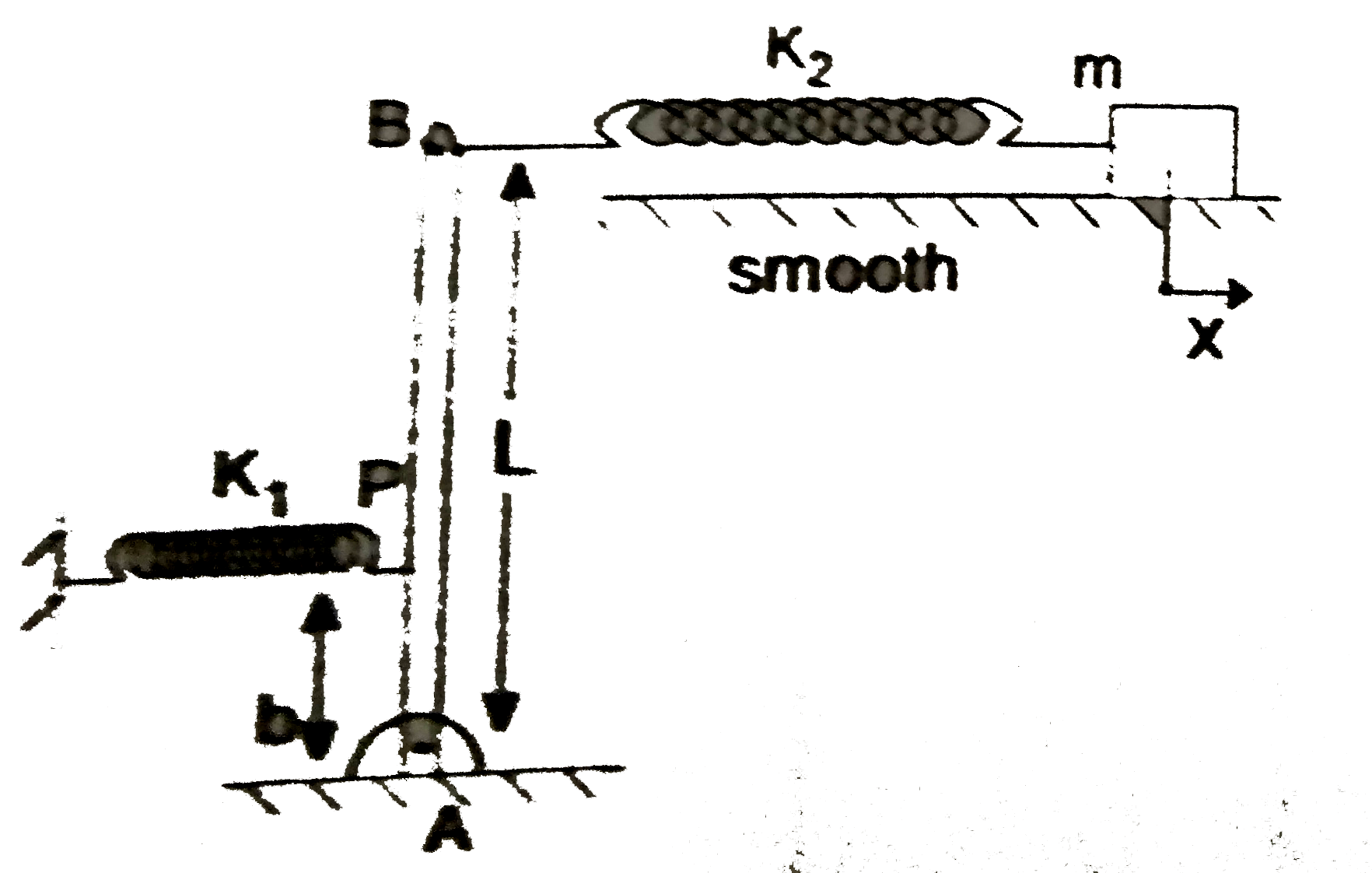A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A massless Rod AB is hinged at point A. At point P, it is connected by...
Text Solution
|
- A rod mass (M) hinged at (O) is kept in equilibrium with a spring of s...
Text Solution
|
- A body of mass m hangs from a smooth fixed pulley P(1) by the inextens...
Text Solution
|
- In the figure shown, the spring are connected to the rod at one end an...
Text Solution
|
- Find the frequency of small oscillatinos of a thin uniform vertical ro...
Text Solution
|
- A block of mass is connected to an ideal spring of stiffness K(1) on l...
Text Solution
|
- Two particles each of mass m are attached at end points of a massless ...
Text Solution
|
- Two springs of spring constant k(1)and k(2) are connected by a mass m ...
Text Solution
|
- Two spring of spring constants k(1) and k(2) ar joined and are connect...
Text Solution
|