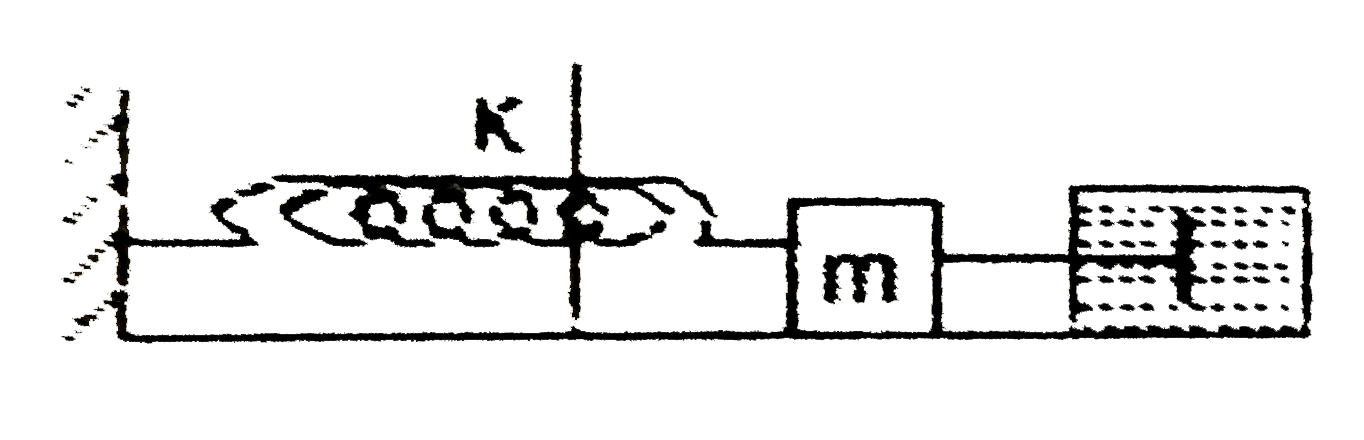A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- For a damped oscillator which follow the equation vecF=-kvecx-bvecV ...
Text Solution
|
- A particle oscillating under a force vecF=-kvecx-bvecv is a (k and b a...
Text Solution
|
- For a damped oscillation of a particle, show that time taken for the a...
Text Solution
|
- Calculate the time taken for particele energy to drop to half its init...
Text Solution
|
- For the damped oscillator shown in Fig. 14.19, the mass m of the block...
Text Solution
|
- For the damped oscillator shown in Fig. 14.19, the mass m of the block...
Text Solution
|
- For the damped oscillator, the mass m of the block is 200g, k = 90 Nm^...
Text Solution
|
- For the damped oscillator, the mass m of the block is 200g, k = 90 Nm^...
Text Solution
|
- For the damped oscillator, the mass m of the block is 400g, k = 120 Nm...
Text Solution
|