A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
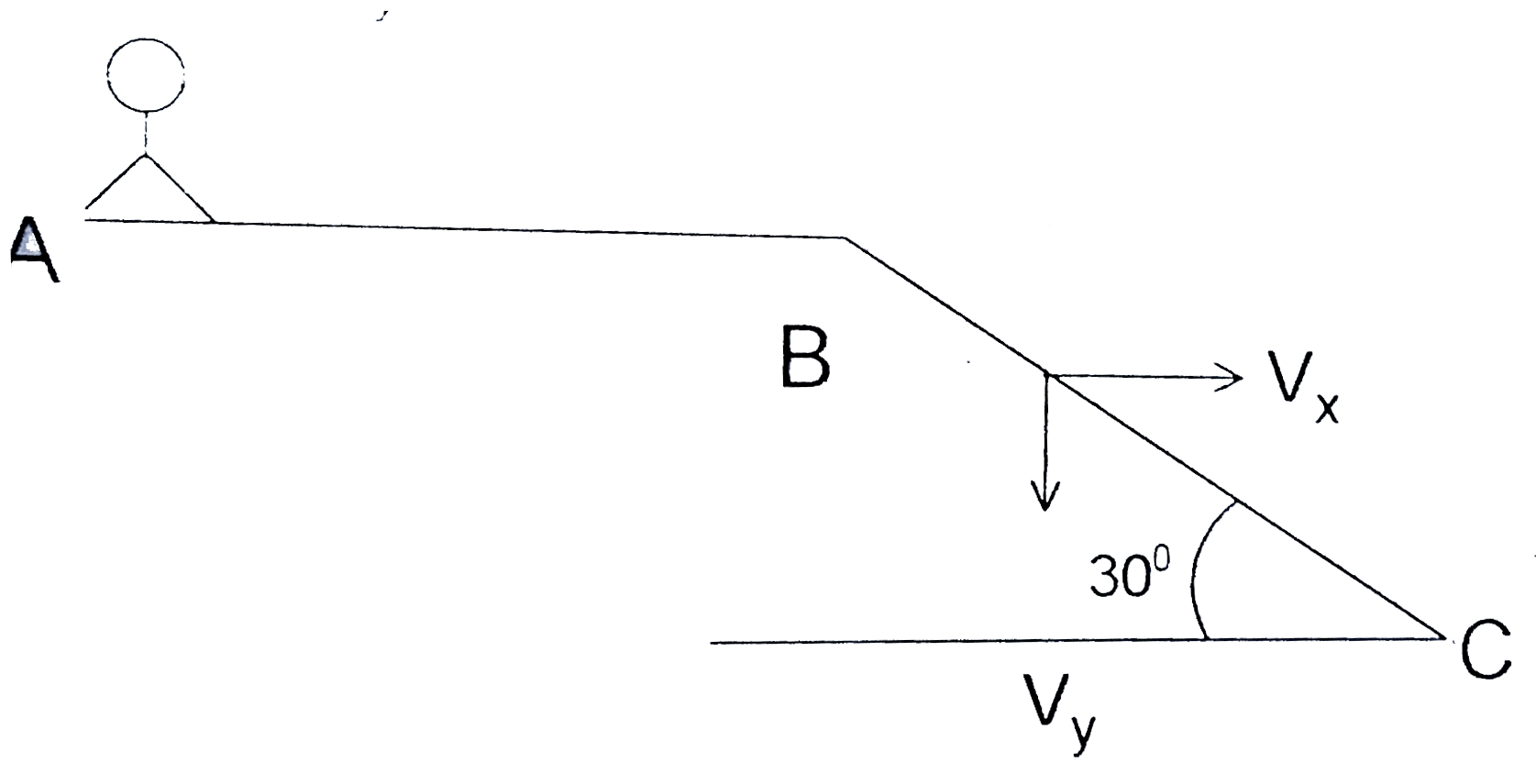
- A man moving on track ABC, getting rain drops vertical for the path AB...
Text Solution
|
- Rain is falling with a sped of 12sqrt(2)m//s at an angle 45^@ with the...
Text Solution
|
- A man moving in rain holds his unbrella inclined to the vertical even ...
Text Solution
|
- A stone is just dropped from the window of a train moving along a hori...
Text Solution
|
- Rain is falling with speed 12sqrt(2) m//s at an angle of 45^(@) with v...
Text Solution
|
- A man walking with a speed of 3 km/h finds the rain drops falling vert...
Text Solution
|
- A man moving in rain holds his umbrella inclined to the vertical even ...
Text Solution
|
- A car with a vertical windshield moves in a rain storm at a speed of 4...
Text Solution
|
- A man moving with a speed v down the inclined plane meets the rain hor...
Text Solution
|