Home
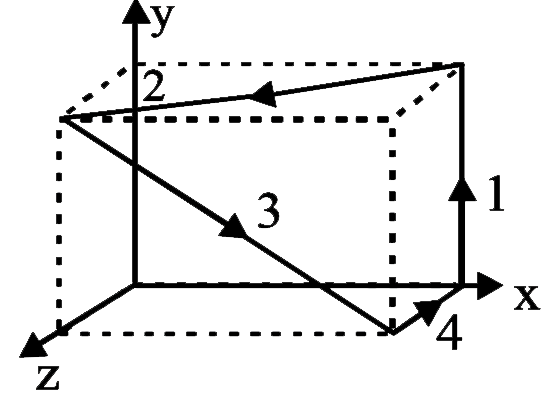
Class 12
PHYSICS
A wire carrying a 10 A current is bent t...

A wire carrying a 10 A current is bent to pass through sides of a cube of side 10 cm as shown in figure. A magnetic field `vec(B) = (2 hat(i) - 3 hat(j) +hat (k))T` is present in the region. Then, find

The net torque on the loop

A

a.`sqrt20xx10^(-1)Nm`

B

b.`sqrt20xx10^(-2)Nm`

C

c.`sqrt150xx10^(-2)Nm`

D

d.`sqrt150xx10^(-2)Nm`

Text Solution

Verified by Experts

The correct Answer is:
A
`vec(M)=10{100xx10^(-4)hat(i)+50xx10^(-4)hat(j)+50xx10^(-4)hat(k)}`
`=(10hat(i)+5hat(j)+5hat(k))xx10^(-3)Am^(2)`
`vec(B)=2hat(i)-3hat(j)+hat(k)`
`vectau=vec(M)xxvec(B)=10xxsqrt20xx10^(-2)Nm=sqrt20xx10^(-1)Nm`
Promotional Banner

Similar Questions

Explore conceptually related problems

A wire carrying a 10A current is bent to pass through various sides of a cube of side 10 cm as shown in fig. A magnetic field vecB=(2hati-3hatj+hatk)T is present in the region. Find the net torque on the loop.

A wire carrying a 10A current is bent to pass through various sides of a cube of side 10 cm as shown in fig. A magnetic field vecB=(2hati-3hatj_)T is present in the region. Find the net force on the loop shown.

A wire carrying a 10A current is bent to pass through various sides of a cube of side 10 cm as shown in fig. A magnetic field vecB=(2hati-3hatj-hatk)T is present in the region. Find the magnetic moment vector of the loop.

A wire loop carrying current I is placed in the x-y plane as shown in the figure. If an external uniform magnetic field vec(B)=B hat(i) is switched on, then the torque acting on the loop is

If vec(a) = hat(i) - 2 hat(j) + 3 hat(k) and vec(b) = 2 hat(i) - 3 hat(j) + 5 hat(k) , then angle between vec(a) and vec(b) is

A magnet of magnetic moment 50 hat(i) A-m^(2) is placed along the x-axis in a magnetic field vec(B)=(0.5hat(i)+3.0hat(j))T . The torque acting on the magnet is

A "bar" magnet of moment vec(M)=hat(i)+hat(j) is placed in a magnetic field induction vec(B)=3hat(i)+4hat(j)+4hat(k) . The torque acting on the magnet is

A charged particle has acceleration vec a = 2 hat i + x hat j in a megnetic field vec B = - 3 hat i + 2 hat j - 4 hat k. Find the value of x.

If vec(A)=2hat(i)+3hat(j)-hat(k) and vec(B)=-hat(i)+3hat(j)+4hat(k) , then find the projection of vec(A) on vec(B) .

The figure shows a loop of wire carrying a current i as shown. There exists a uniform magnetic field along x-axis given by vec(B) = B_(0) hat(i) . If the length of each side is a, then