Home
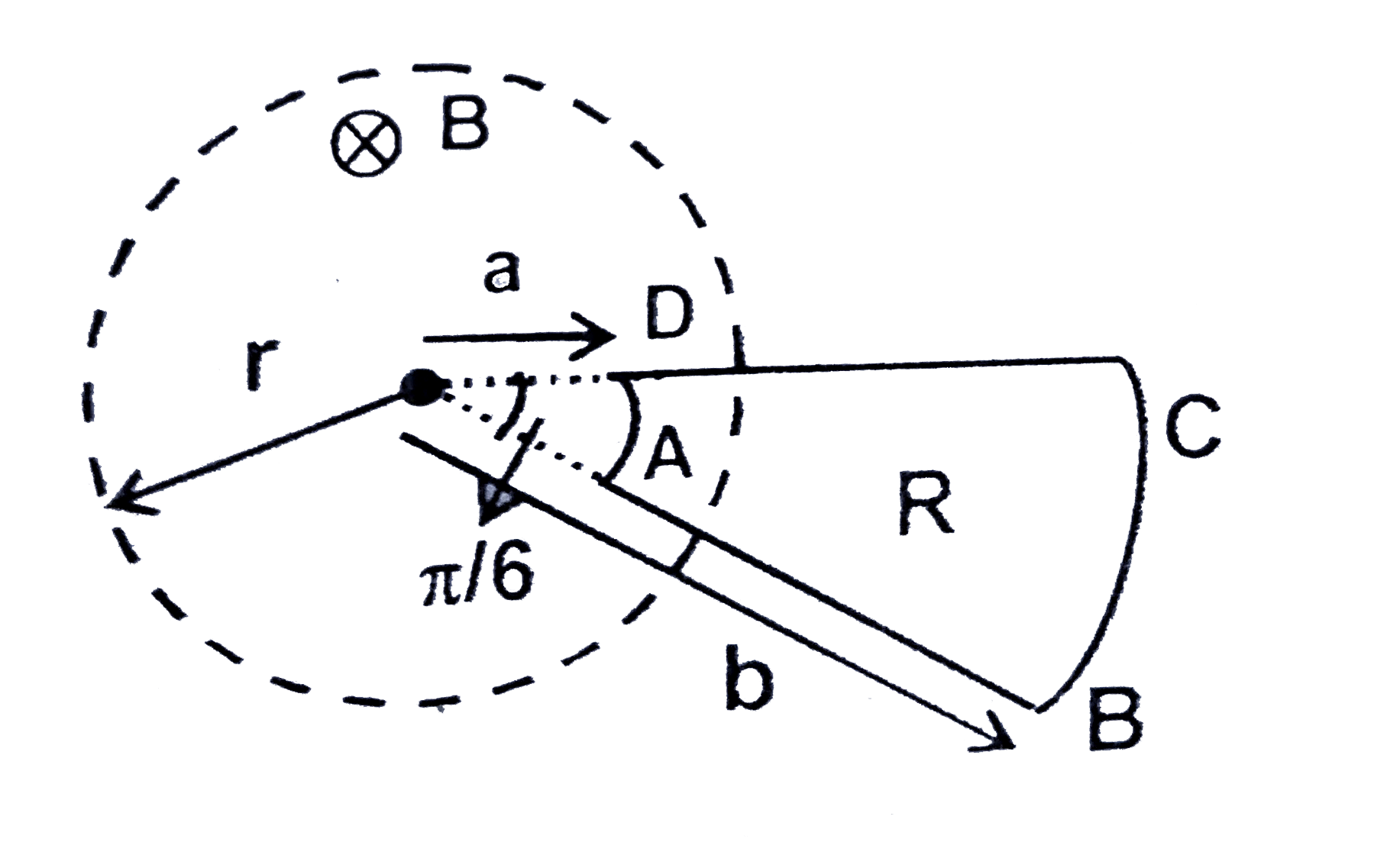
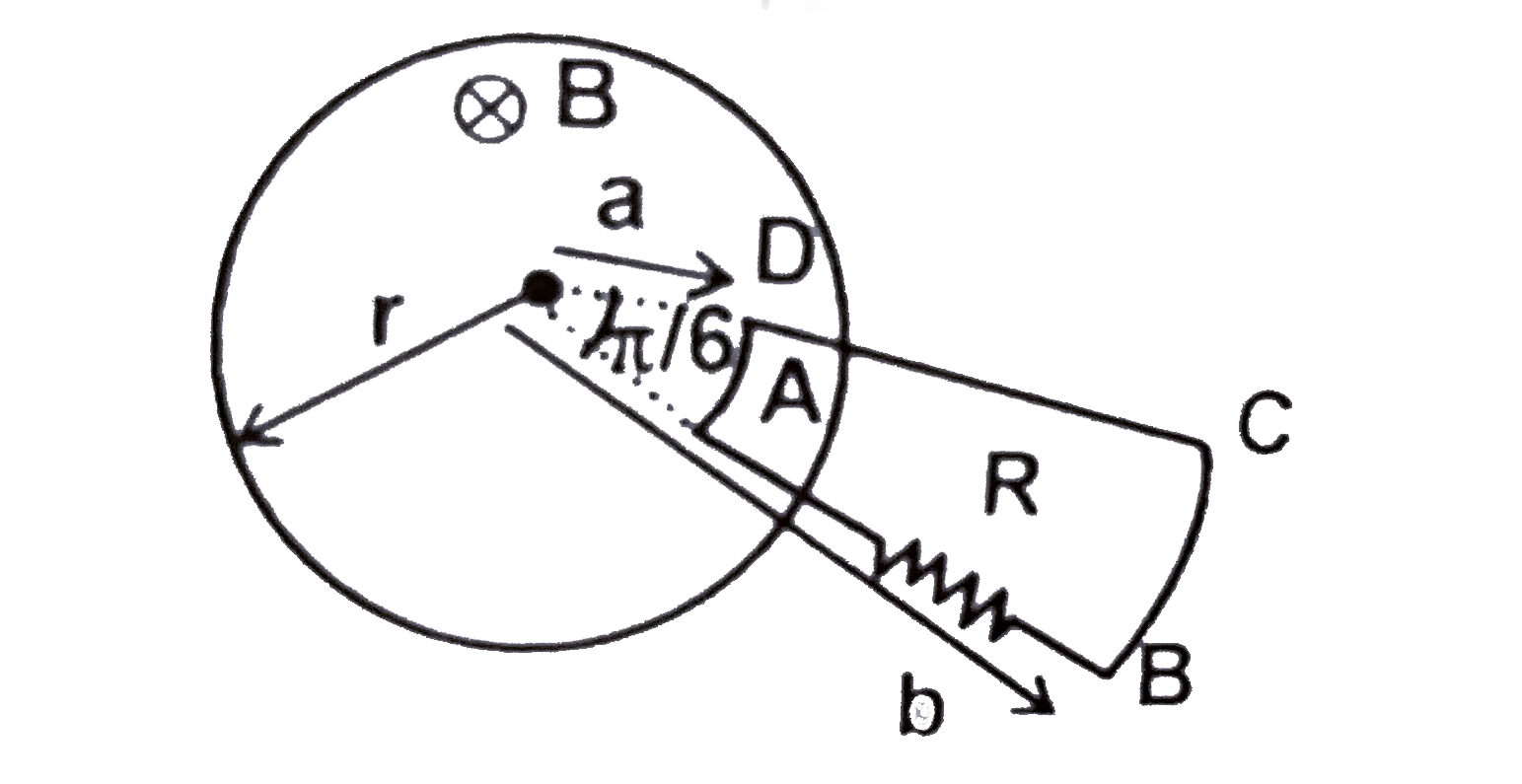
Class 12
PHYSICS
Magnetic field B in a cylindrical region...

Magnetic field B in a cylindrical region of radius r varies according to the law `B = B_(0)t` as shown in the figure. A fixed conducting loop ABCDA of resistance R is lying in the region as show . The current flowing through the loop is

A

`(pia^(2)B_(0))/(12R)`

B

`(pi(r^(2)-a^(2))B_(0))/(12R)`

C

`(pi(b^(2) - a^(2))B_(0))/(12R)`

D

none of the above

Text Solution

Verified by Experts

The correct Answer is:
B
`e=(dphi)/(dt)=((r^(2)-a^(2)))/(2)(pi)/(6)(dB)/(dt)`
`:. i = ((r^(2)-a^(2))piB_(0))/(12R)`
Promotional Banner

Similar Questions

Explore conceptually related problems

Magnetic field in cylindrical region of radius R in inward direction is as shown in figure.

Magnetic field in the cylindrical regaion with its axis passing through O varies at a constant rate (dB)/(dt) . A treangular imaginary loop ABC, with AB = BC , is lying in this region as shown in the adjacent figure. The work done to move unit positive charge from A to B along the side AB is

There exists a uniform magnetic field bar B = B_(0)t bar k in a region. A circular conducting loop of radius r and resistance R is placed with its plane in x-y plane. Determine the current through the loop and sense of the current.

A current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is

A non uniform magnetic field B=B_(0)that"i" in a region exists. A circular conducting loop of radius r and resistance R is placed with its plane in yz-plane. Determine the current through the loop and sense of the current.

A stationary circular loop of radius a is located in a magnetic field which varies with time from t = 0 to t = T according to law B = B_(0) t(T - t) . If plane of loop is normal to the direction of field and resistance of the loop is R, calculate magnitude of charge flown through the loop from instant t = 0 to the instant when current reverses its direction.

A uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

A current carrying circular loop of radius R is placed in a uniform magnetic field B_(0) Tesla in x-y plane as shown in figure. The loop carries a current i = 1A in the direction shown. Find the torqure acting on the loop

The flux of electric field through the circular region of radius r as shown in the figure is