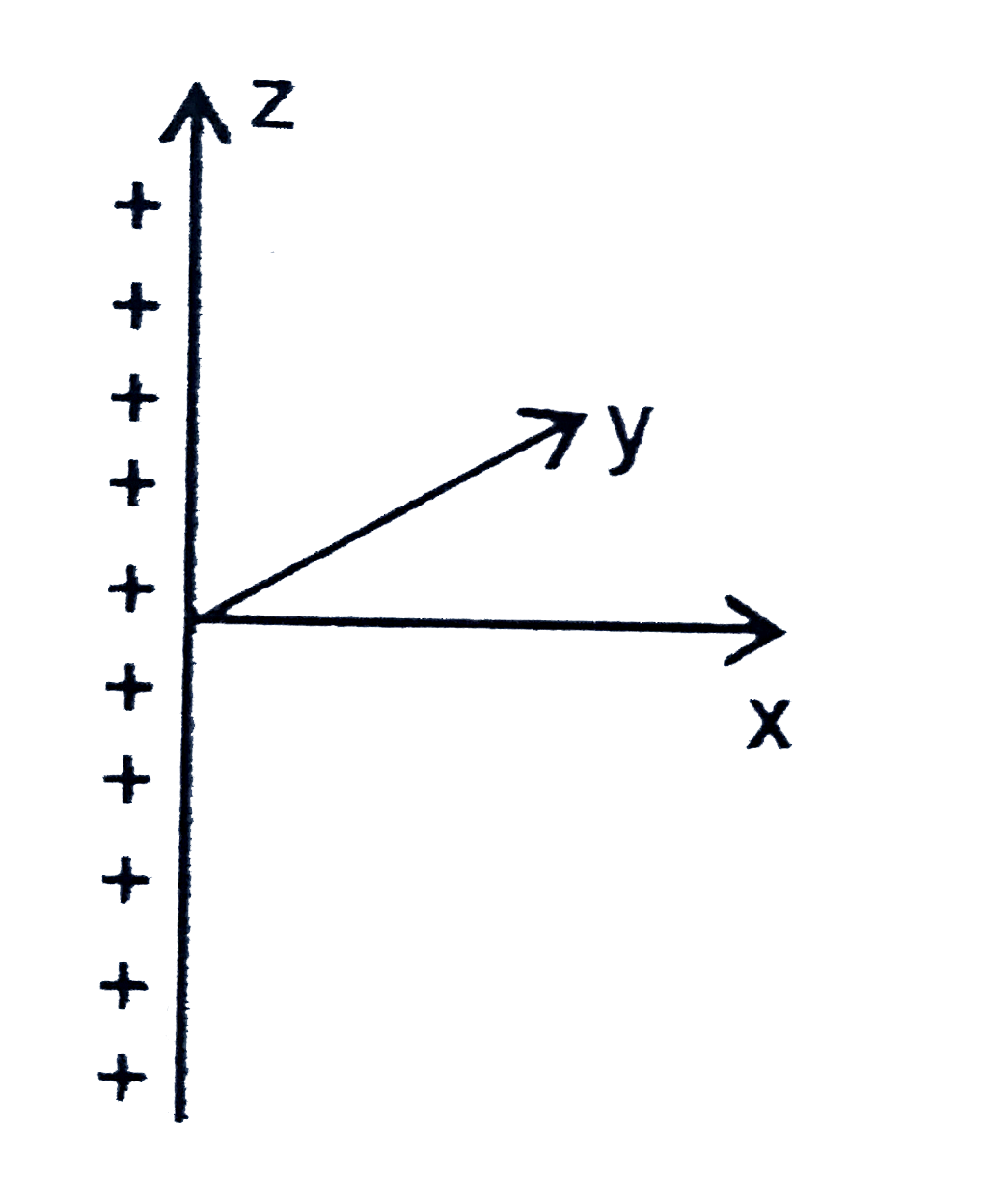A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An infinite thread of charge density lambda lies along z-axis. The pot...
Text Solution
|
- There is infinitely long straight thread carrying a charge with linear...
Text Solution
|
- Find electric field at point A, B, C, D due to infinitely long uniform...
Text Solution
|
- If the points A(3, 9, 4), B(0, -1, -1), C(lambda, 4, 4), D(4, 5, 1) ar...
Text Solution
|
- [" An infinite number of "],[" charges each equal "],[" to 'q' are pla...
Text Solution
|
- An infinitely long line of linear charge density lambda is shown in th...
Text Solution
|
- An infinite conducting sheet has surface charge density sigma. The dis...
Text Solution
|
- Find ratio of electric at point A and B. Infinitely long uniformly cha...
Text Solution
|
- The distance between the plane x-2y+z-6=0 and the plane containing the...
Text Solution
|