Home
Class 12
PHYSICS
A cell is connected between the points A...

A cell is connected between the points A and C of a circular conductor ABCD of centre `'O'.angle AOC = 60^(@)`. If` B_(​1) and B_(​2)` are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio `(B_(1))/(B_(2))`, is

A

5

B

`1//5`

C

6

D

1

Text Solution

Verified by Experts

The correct Answer is:
D
Let lengths of ABC and ADC is `l_(1)` and `l_(2)` respectively. Then
`(_(1))/(l_(2)) = (360 - 60)/(60) = 5` Now `(i_(1))/(i_(2)) = (l_(1))/(l_(2)) = :. i_(2) = 5i_(1)`
Now `B_(1) = (5)/(6) ((mu_(o)i_(1))/(2r))` and `B_(2) = (1)/(6) ((mu_(o)i_(2))/(2r))`
Promotional Banner

Similar Questions

Explore conceptually related problems

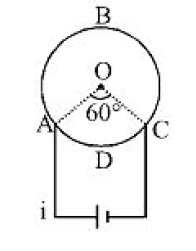
A cell is connected between the point A and C of a circular conductor ABCD of centre O, /_AOC = 60^(@) . If B_(1_ and B_(2) are the magnitude of magnetic fields at O due to the currents in ABC and ADC respectively, the ratio of B_(1)//B_(2) is.

The magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :

The figure shows tow coaxial circulalr loop a1 and 2, which forms same solid angle theta at point O . If B_1 and B_2 are the magnetic fields produced at the point O due to loop 1 and 2 respectively, then

A magnetic compass needl oscillates 30 times per minute at a place where the dip is 45^(@) and 40 times per minute where the dip is 30^(@) if B_(1) and B_(2) are respectively the total magnetic field due to the earth at the two places then the ratio B_(1)//B_(2) is best given by

A and B are two concentric circular conductors of centre O and carrying currents i_(1) and i_(2) as shown in the adjacent figure. If ratio of their radii is 1:2 and ratio of the flux densities at O due to A and B is 1:3 , then the value of i_(1)//i_(2) is

As shown in figure a cell is connected across two points A and B of a uniform circular conductor of radius r. Prove that the magnetic field induction at its centre O will be zero.

Two coils are having magnetic field B and 2B at their centres and current i and 2i then the ratio of their radius is

Torques tau_(1) and tau_(2) are required for a magnetic needle to remain perpendicular to the magnetic fields at two different places. The magnetic field at those places are B1 and B2 respectively, then (B_(1))/(B_(2)) is

The dipole moment of a circular loop carrying a current I, is m and the magnetic field at the centre of the loop is B_(1) . When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is B_(2) . The ratio (B_(1))/(B_(2)) is:

The magnetic field at the centre of a circular coil carrying current I ampere is B. It the coil is bent into smaller circular coil of n turns then its magnetic field at the centre is B, the ratio between B' and B is