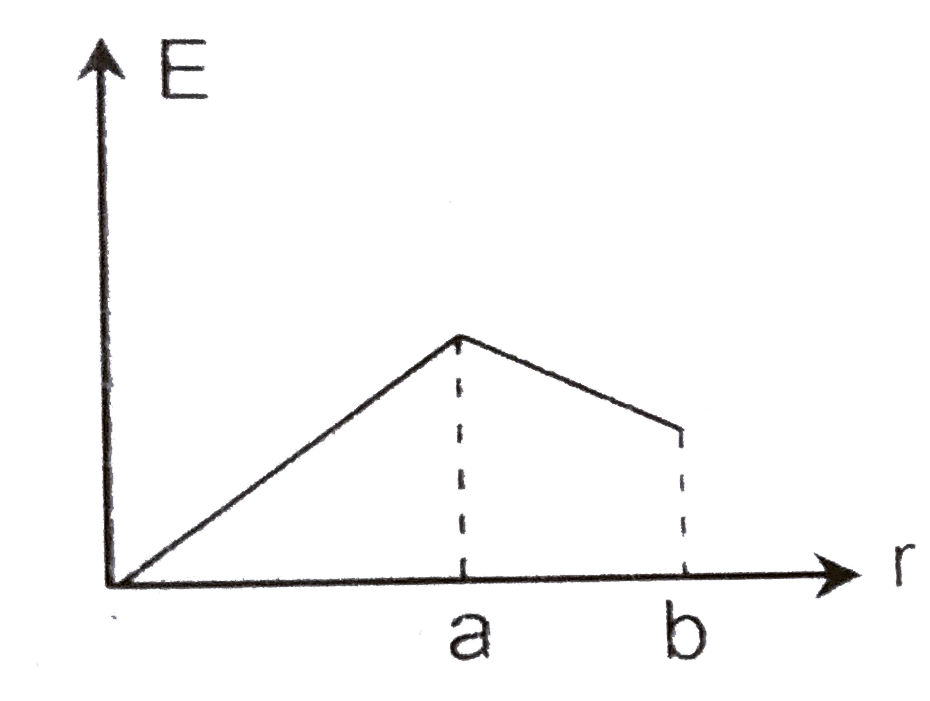
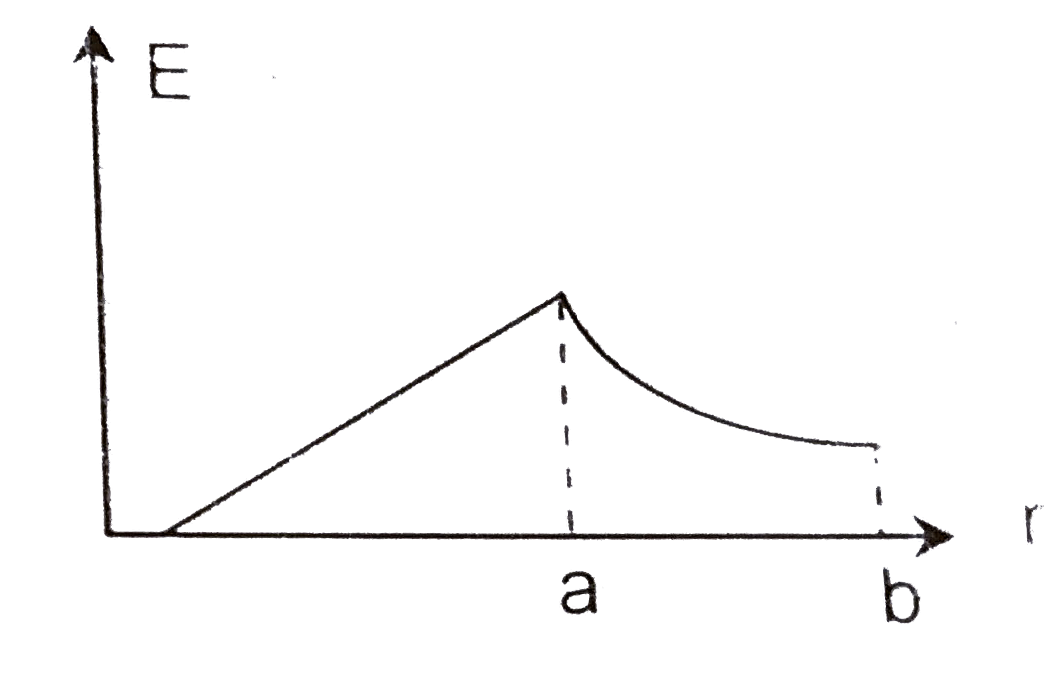
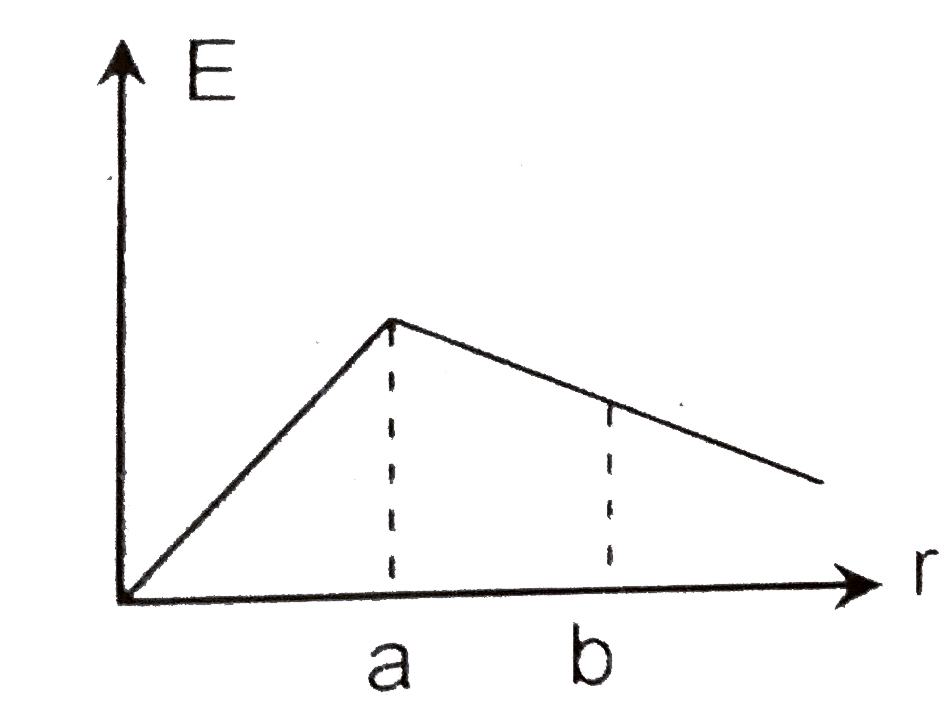
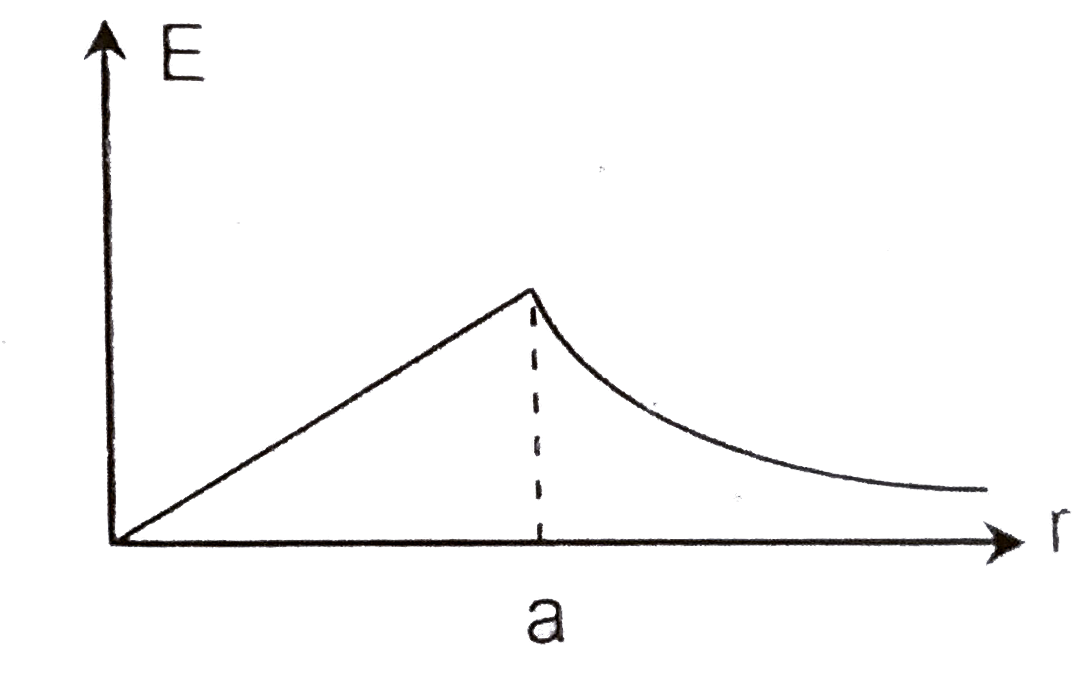
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A capacitor is made of two concentric spherical shells A and B of radi...
Text Solution
|
- Three concentric spherical shells have radii a, b and c(a lt b lt c) a...
Text Solution
|
- Three concentric spherical shells have radii a,b and c(a lt b lt c) an...
Text Solution
|
- In an arrangement of two concentric conducting shells, with centre at ...
Text Solution
|
- Three concentric metal shells A, B, and C of respective radii a,b and ...
Text Solution
|
- धातु के तीन संकेन्द्रीय कोशों A, B, C की त्रिज्याएँ क्रमशः a, b, c तथा...
Text Solution
|
- In an arrangement of two concentric conducting shells, with centre at ...
Text Solution
|
- There are four concentric spherical shells A, B, C and D of radii R, 2...
Text Solution
|
- Two thin cocentric and coplanar spherical shells , of radii 'a' and '...
Text Solution
|