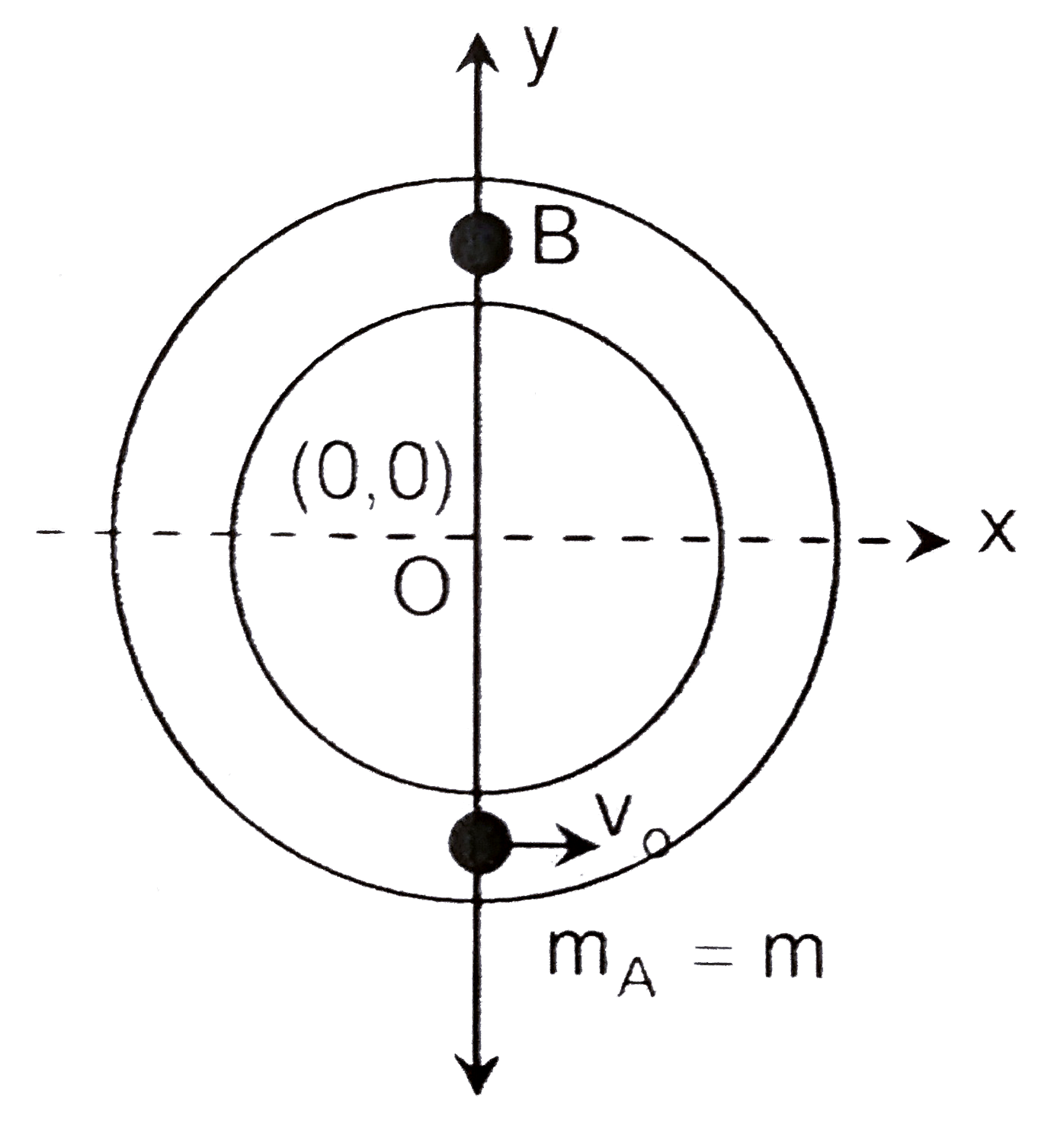
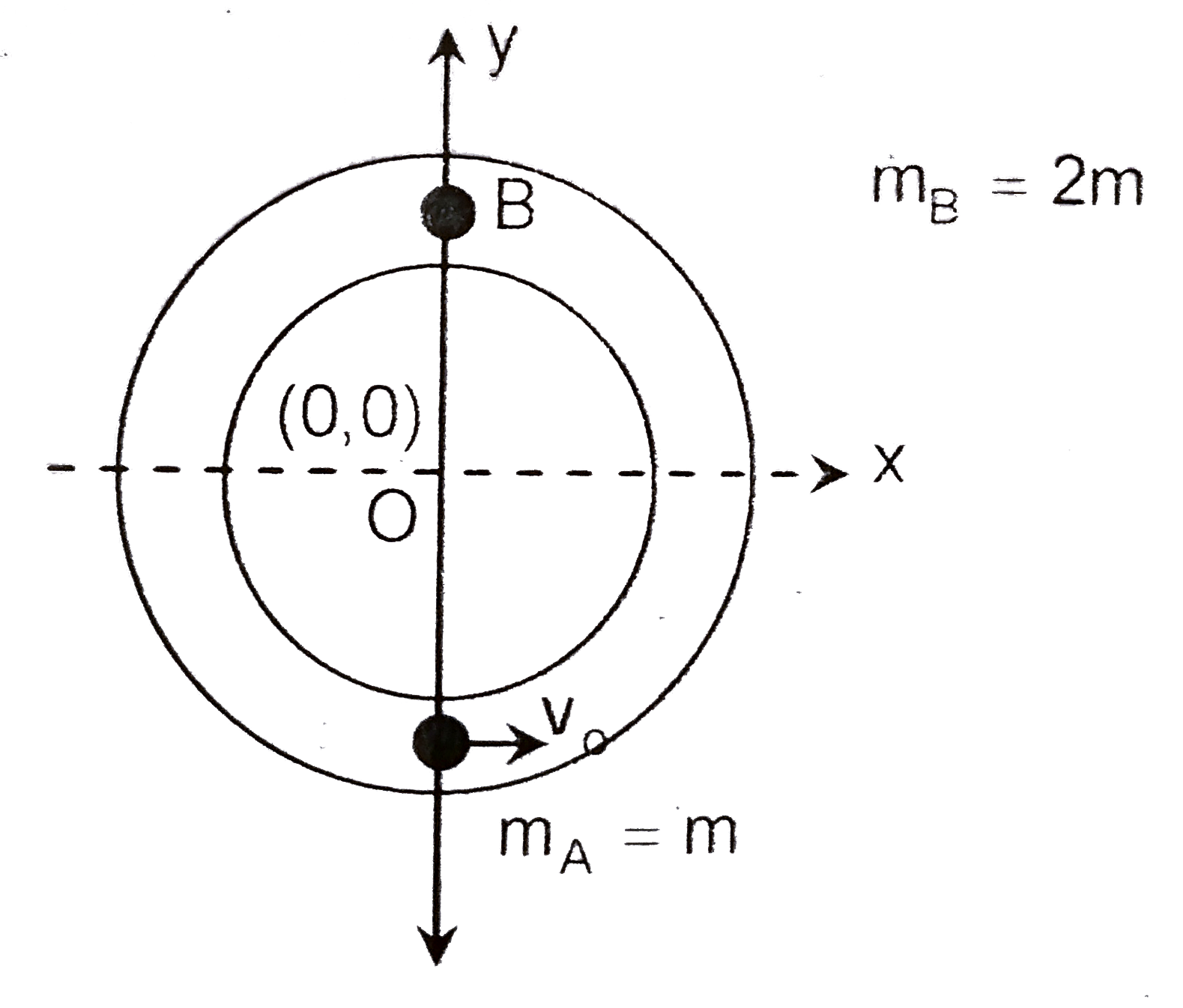
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A hollow circular tube of radius R and negligible internal diameter is...
Text Solution
|
- A heavy ball of mass 2M moving with a velocity v(0) collides elastical...
Text Solution
|
- Two smooth balls A and B, each of mass m and radius R, have their cent...
Text Solution
|
- Two smooth balls A and B , each of mass m and radius R , have their ce...
Text Solution
|
- Two balls each of mass 'm' are moving with same velocity v on a smooth...
Text Solution
|
- A ball of mass M moving with a velocity v collides perfectly inelastic...
Text Solution
|
- Two balls marked 1 and 2 of the same mass m and a third ball marked 3 ...
Text Solution
|
- A point mass m collides with a disc of mass m and radius R resting on ...
Text Solution
|
- A billiard ball of mass M , moving with velocity v1 collides ...
Text Solution
|