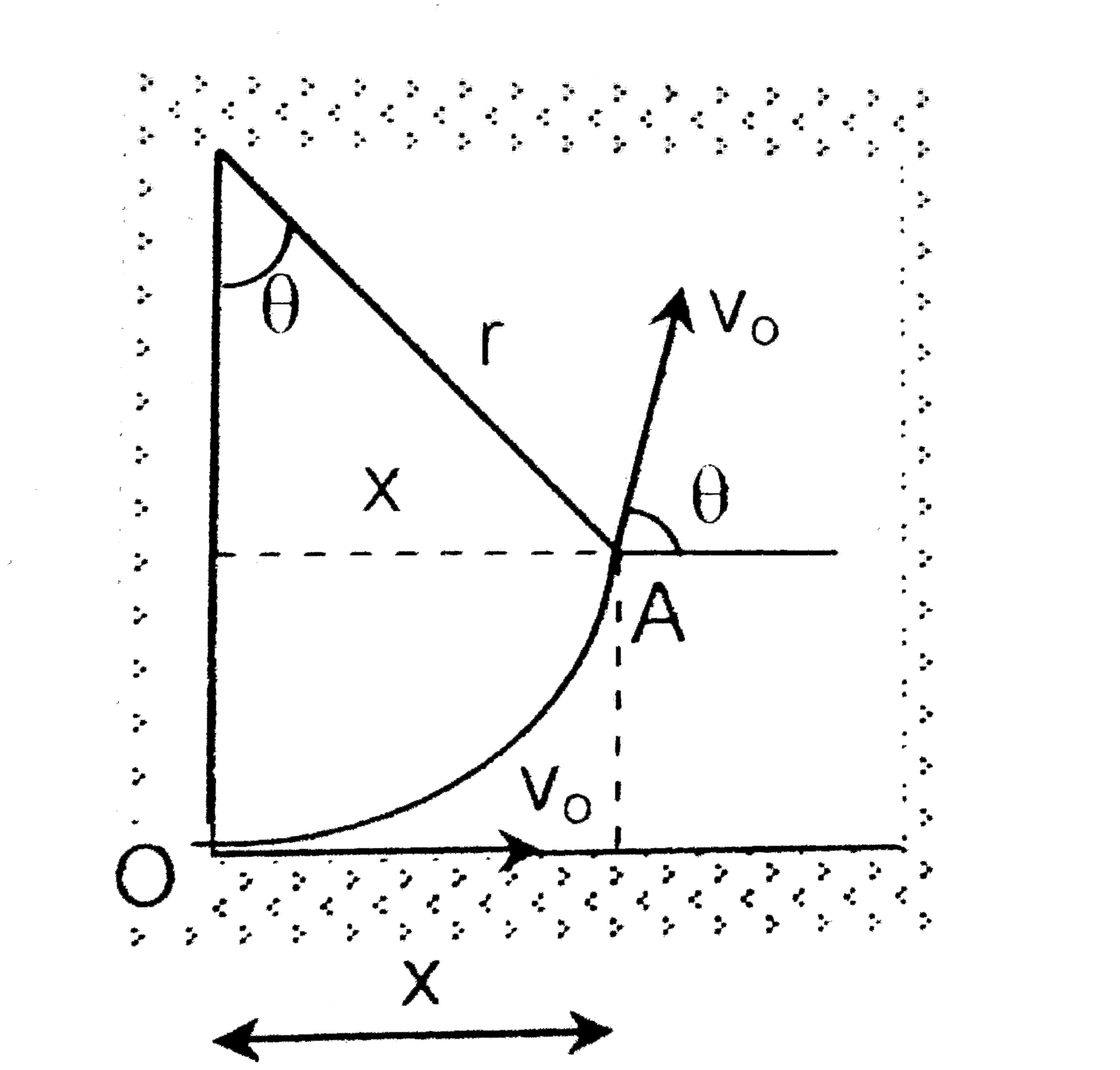A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Choose the correct option: A particle of charge per unit mass alpha i...
Text Solution
|
- Suppose a nucleus initally at rest undergoes alpha decay according to...
Text Solution
|
- A particle of charge per unit mass alpha is released from origin with ...
Text Solution
|
- A particle of charge per unit mass alpha is released from origin with ...
Text Solution
|
- The position of a particle at time t, is given by the equation, x(t) =...
Text Solution
|
- A charged particle of specific charge (Charge/mass) alpha is released ...
Text Solution
|
- A particle of specific charge 'alpha' is projected from origin at t=0 ...
Text Solution
|
- A charge praticule of sepeific charge (charge/ mass ) alpha is realsed...
Text Solution
|
- A charged particle (q.m) released from origin with velocity v=v(0)hati...
Text Solution
|