Home
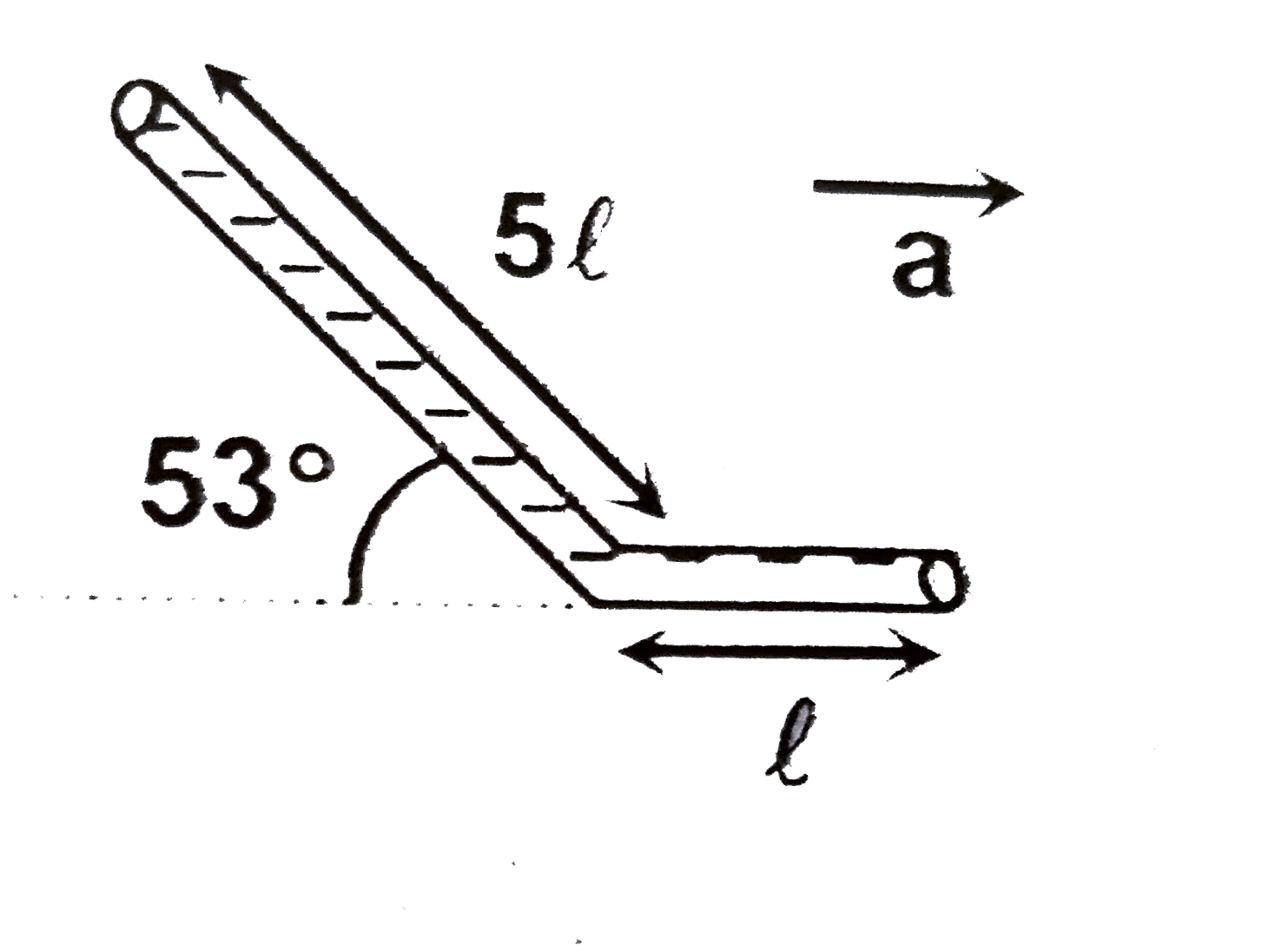
Class 12
PHYSICS
In the given tube liquid density rho is ...

In the given tube liquid density `rho` is filled. Find the acceleration of the tuve towards right direction such that no liquid will fall out of the tube.

A

`(3)/(5)g`

B

`(4)/(5)g`

C

`g`

D

`4g`

Text Solution

Verified by Experts

The correct Answer is:
C
`tan theta = (4l)/(4l) = (a)/(g)`
`rArr a = g`
Or, `PA - P_(0)A = (rholA)a`
`(5l) (rhoA) ("g" (4)/(5) - (3)/(5) a) = rhol rhoa`
`a = g`
Promotional Banner

Similar Questions

Explore conceptually related problems

A vertical U -tube has two liquids 1 and 2 . The heights of liquids columns in both the limbs are h and 2h , as shown in the figure. If the density of the liquid 1 is 2rho . a. Find the density of liquid 2 . b. If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.

An ideal liquid of density rho is pushed with velocity v through the central limb of the tube shown in fig. What force does the liquid exert on the tube? The cross sectional areas of the three limbs are equal to A each. Assume stream-line flow.

A narrow tube completely filled with a liquid is lying on a series of cylinders as shown in the figure. Assuming no sliding between any surfaces, the value of acceleration of the cylinders for which liquid will not come out of the tube from anywhere is given by

A container contains an incompressible and non - viscous liquid of density rho and is filled upto a height H . Now if container is moved towards right with an acceleration a then find the horizontal force exerted by liquid on the face ABCD of container . Assume container have enough height so that liquid does not fall outside the container .

A tube in vertical plane is shown in figure. It is filled with a liquid of density rho and its end B is closed. Then the force exerted by the fluid on the tube at end B will be: [Assume the radius of the tube to be negligible in comparison to l]

A liquid of density rho is filled in a U-tube is accelerated with an acceleration a so that the height of liquid in its two vertical arms are h_1 and h_2 as shown in the figure. If l is the length of horizontal arm of the tube, the acceleration a is

A block of volume V and density rho is floating in a liquid of density 2 rho filled in a vessel. Now the vesset starts falling freely with acceleration g . Then the volume of block inside the liquid in the falling condition is

A non viscous liquid of density rho is filled in a tube with A as the area of cross section, as shown in the figure. If the liquid is slightly depressed in one of the arms, the liquid column oscillates with a frequency

A beaker containing a liquid of density rho moves up with an acceleration a . The pressure due to the liquid at a depth h below the free surface of the liquid is.

A vertical U tube contains a liquid of density rho , length of the liquid in the tube is 2H. The liquid is displaced slightly and released. Show that the liquid will execute SHM. Also find its time period. Take liquid to be ideal.