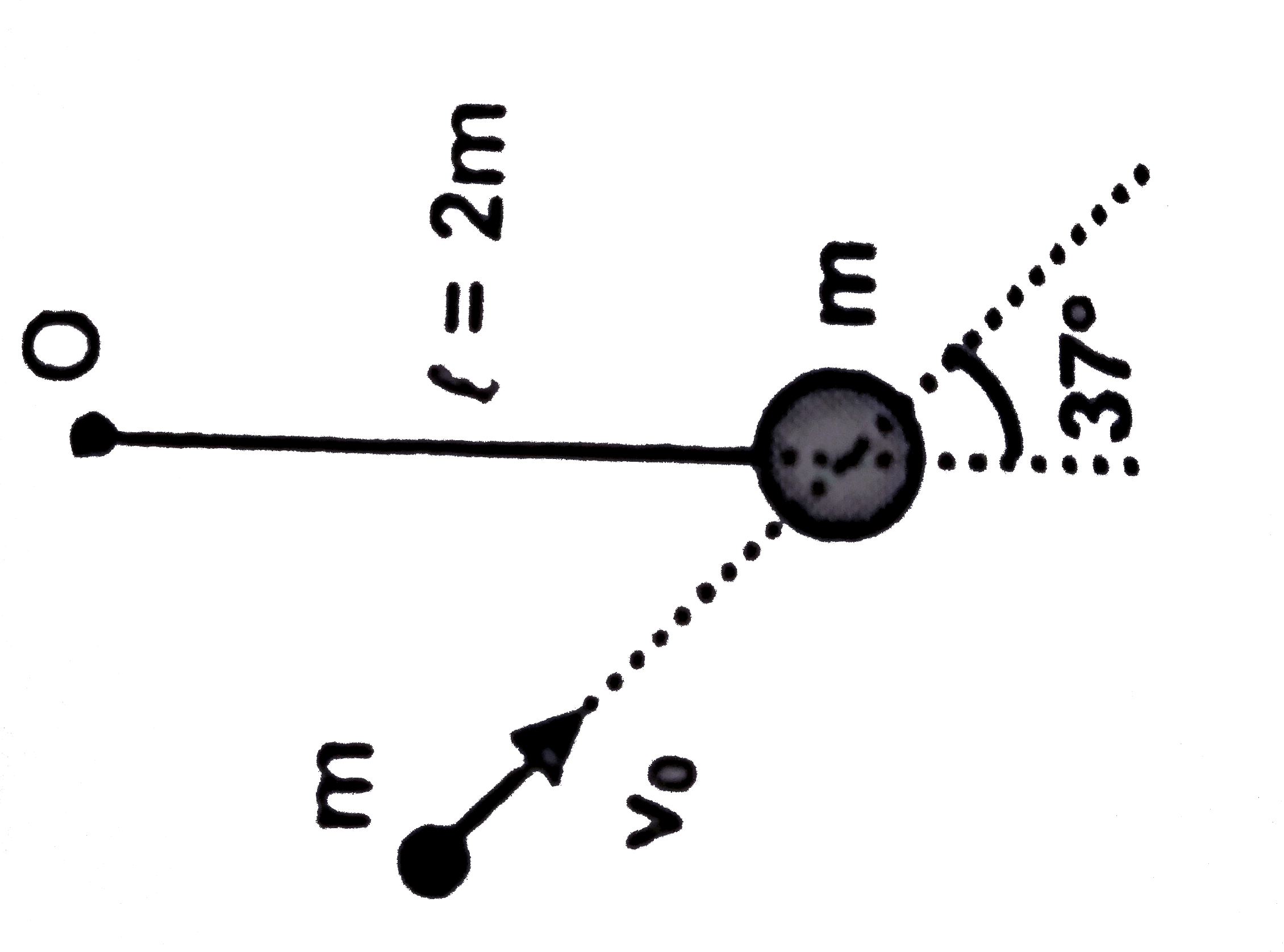
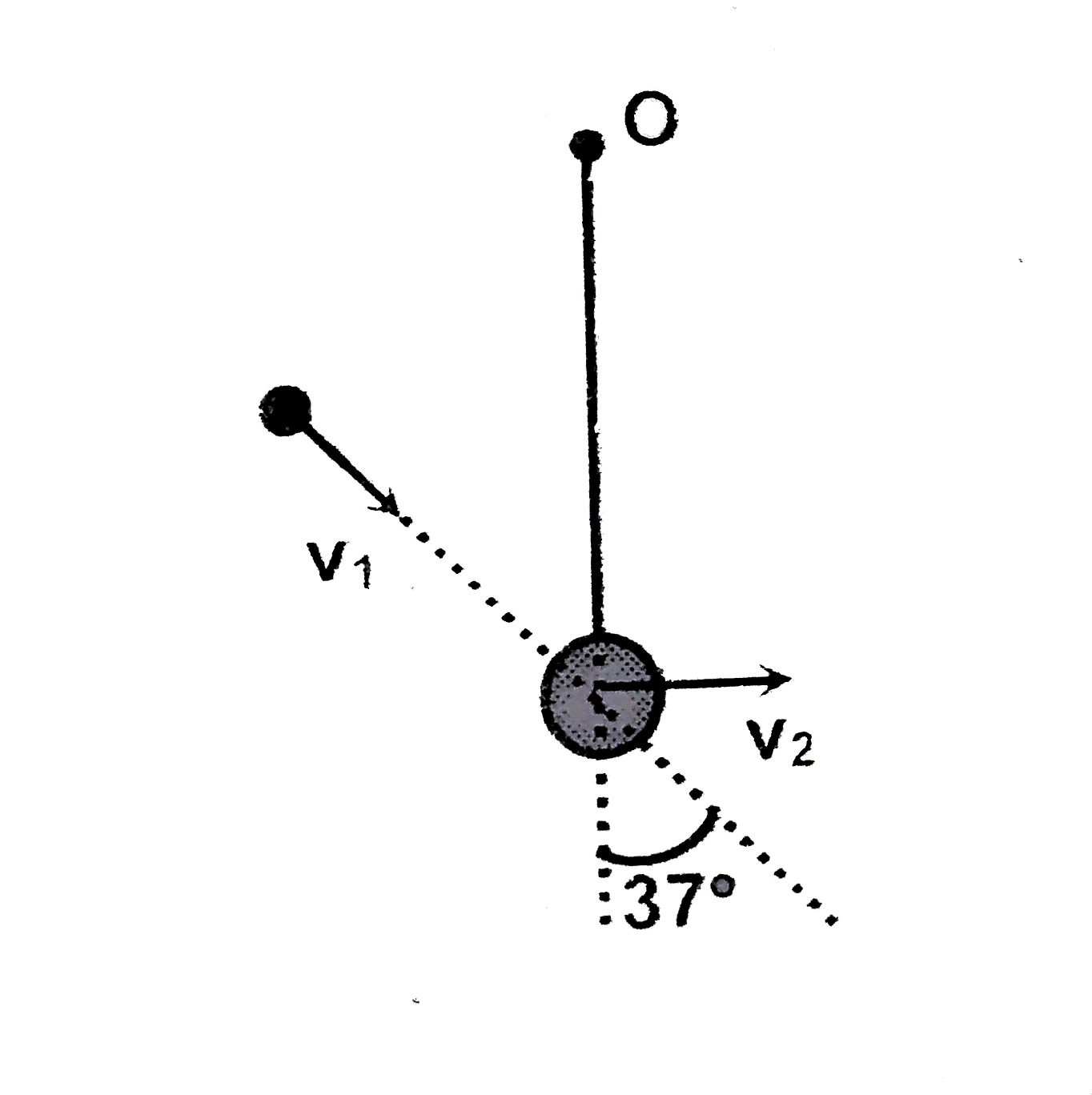
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An elastic ball of mass 'm' is suspended from a fixed point 'O' by an...
Text Solution
|
- A heavy ball of mass 2M moving with a velocity v(0) collides elastical...
Text Solution
|
- A small steel ball A is suspended by an inextensible thread of length ...
Text Solution
|
- Two balls of masses 2 m and m are moving with speed 2 v(0) and v(0) to...
Text Solution
|
- A ball of mass m is attached to the lower end of a vertical string who...
Text Solution
|
- An elastic ball of mass 'm' is suspended from a fixed point by an inex...
Text Solution
|
- An iron ball of mass m , suspended by a light inextensible string of l...
Text Solution
|
- A ball of mass m moving with velocity v collides head-on which the sec...
Text Solution
|
- A billiard ball of mass M , moving with velocity v1 collides ...
Text Solution
|