Home
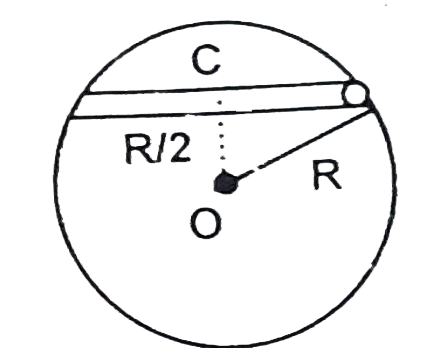
Class 12
PHYSICS
A tunnel is dug across the earth of mass...

A tunnel is dug across the earth of mass 'M' and radius 'R' at a distance `R//2` from the centre 'O' of the Earth as shown. A body is released from rest from one end of the smooth tunnel. The velocity acquired by the body when it reaches the centre 'C' of the tunnel is

A

`sqrt((3GM)/(2R))`

B

`sqrt((3GM)/(4R))`

C

`sqrt((3GM)/(8R))`

D

`dsqrt((3GM)/(16R))`

Text Solution

Verified by Experts

The correct Answer is:
B
Using conservation of energy
`(1)/(2)mv^(2) = -(GMm)/(R ) - ((-11GMm)/(8R))`
`(1)/(2)mv^(2) = (3GMn)/(8R)`
`:. V = sqrt((3GM)/(4R))`
Promotional Banner

Similar Questions

Explore conceptually related problems

A tunnel is dug along a chord of the earth at a perpendicular distance R//2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. A particle is released from one end of the tunnel. The pressing force by the particle on the wall, and the acceleration of the particle vary with x (distance of the particle from the centre) according to

A tunnel has been dug through the centre of the earth and a ball is released in it. It will reach the other end of the tunnel after

A body starts from rest from a point distant r_(0) from the centre of the earth. It reaches the surface of the earth whose radius is R . The velocity acquired by the body is

A body starts from rest from a point distant r_(0) from the centre of the earth. It reaches the surface of the earth whose radius is R . The velocity acquired by the body is

A tunnel is dug along a chord of the earth a perpendicular distance R/2 from the earth's centre. The wall of the tunnel may be assumed to be frictionless. Find the force exerted by the wall on a particle of mass m when it is at a distance x from the centre of the tunnel.

A ball of mass m and radius r rolls inside a hemispherical shell of radius R . It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is. .

The distance of geostationary satellite from the centre of the earth (radius R) is nearest to

A satellite A of mass m is at a distance of r from the centre of the earth. Another satellite B of mass 2m is at distance of 2r from the earth's centre. Their time periode are in the ratio of

A body at rest starts from a point at a distance r (gtR) from the centre of the Earth. If M and R stand for the speed of the body when it reaches the Earth surface is

The distances from the centre of the earth, where the weight of a body is zero and one-fourth that of the weight of the body on the surface of the earth are (assume R is the radius of the earth)