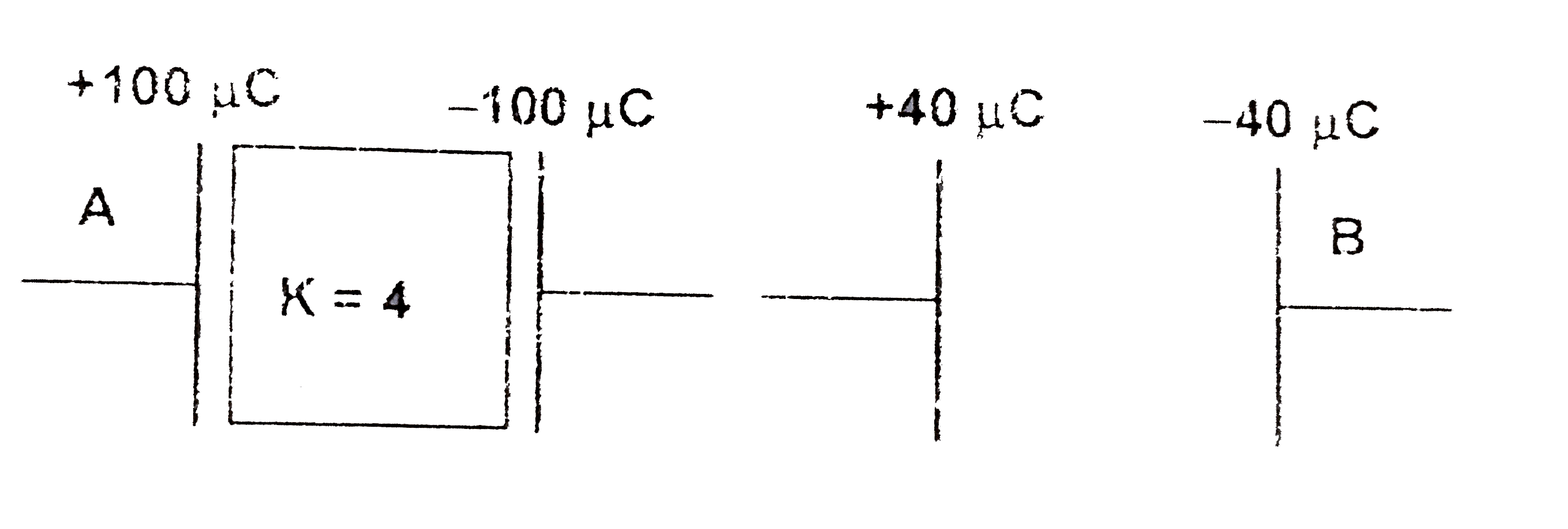A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A parallel plate capacitor 'A' of capacitance 1 muF is charged to a po...
Text Solution
|
- Two parallel plate capacitors of capacitances C and 2C are connected i...
Text Solution
|
- A parallel plate capacitor has area of each plate A, the separation be...
Text Solution
|
- A parallel plate capacitor of capacitance C is charged to a potential ...
Text Solution
|
- Two parallel plate capacitos of capacitences C and 2C are connected in...
Text Solution
|
- 20 muF तथा 30 muF धारिता वाले दो समान्तर प्लेट संधारित्र क्रमश: 30 वो...
Text Solution
|
- Two parallel plate capacitors of capacitances C and 2C are connected i...
Text Solution
|
- A capacitor of capacitance C is charged to potential difference V and ...
Text Solution
|
- A capacitor of capacitance 5 muF is charged to a potential difference ...
Text Solution
|