Home
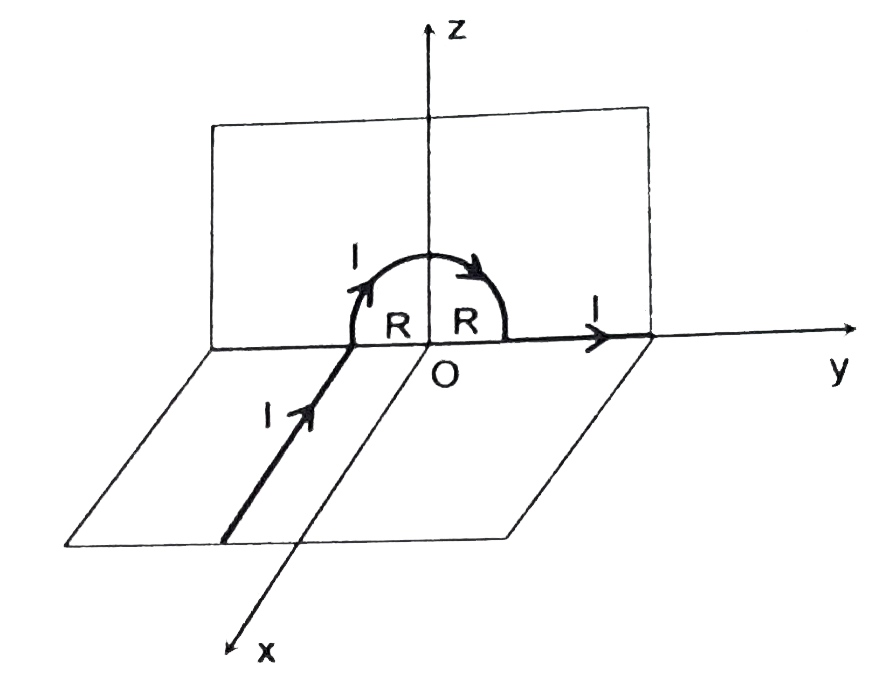
Class 12
PHYSICS
A long wire carrying current 'I' is bent...

A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

A

`(mu_(0)I)/(4piR)sqrt(1 + pi^(2))`

B

`(mu_(0)I)/(4piR)sqrt(2 + pi^(2))`

C

`(mu_(0)I)/(4piR)sqrt(4 + pi^(2))`

D

`(mu_(0)I)/(4piR)sqrt(9 + pi^(2))`

Text Solution

Verified by Experts

The correct Answer is:
A
The net magnetic field intensity at the centre 'O' is
`vec(B_(0)) = (mu_(0)I)/(4piR) (-hat(k)) + (mu_(0)I)/(4R) (-hat(i))`
`:. B_(0) = (mu_(0)I)/(4piR) sqrt(1 + pi^(2))`
Promotional Banner

Similar Questions

Explore conceptually related problems

A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :

A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is

A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R

A current I is flowing through the loop , as shown in the figure . The magnetic field at centre O is

A conductor carrying current I is of the type as shown in figure. Find the magnetic field induction at the common centre O of all the three arcs.

A coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is

In given figure, current I is flowing through straight wire and divided equally in two loops as shown in the figure. The magnitude of magnetic field intensity at the center (O) is

A conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

A conducting wire MN carrying a current I is bent into the shape as shown and placed in xy plane. A uniform magnetic field vecB=-Bhatk is existing in the region. The net magnetic force experenced by the conducting wire MN is

A current carrying wire AB of the length L is turned along a circle, as shown in figure. The magnetic field at the centre O.