A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
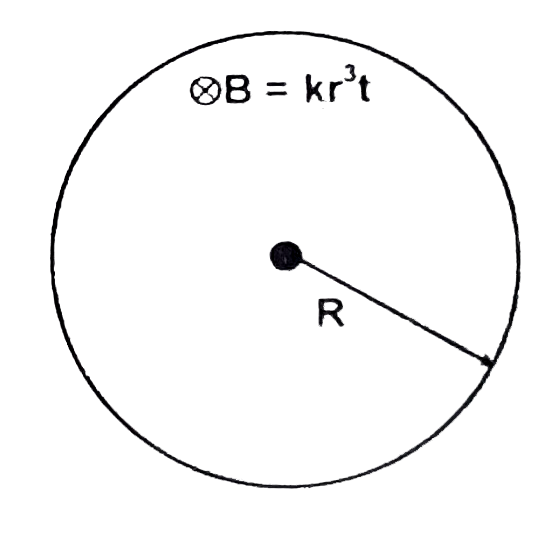
- A time varying magnetic field B = Kr^(3)t is existing in a cylindrical...
Text Solution
|
- A uniform but time-varying magnetic field B(t) exists in a circular re...
Text Solution
|
- A uniform but time varying magnetic field B(t) exist in a circular reg...
Text Solution
|
- Magnetic field in cylindrical region of radius R in inward direction i...
Text Solution
|
- A uniform but time varying magnetic field B=(2t^3+24t)T is present in ...
Text Solution
|
- A time varying magnetic field B=krt (where k is a constant r is the ra...
Text Solution
|
- A uniform but time-varying magnetic field B (t) exists in a circular r...
Text Solution
|
- Find the magnitude of induced filed " E(n) " at a point r (>R) where a...
Text Solution
|
- A uniform but time varying magnetic field B(t) exists in a circular re...
Text Solution
|