Home
Class 12
PHYSICS
A man observes a coin placed at the bott...

A man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.

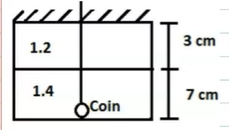
Text Solution

Verified by Experts

The correct Answer is:
8
`[8]`
`d=3.6/1.2+7/1.4=8`
Promotional Banner

Similar Questions

Explore conceptually related problems

A coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.

A concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index mu upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be

A coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?

Two liquids which do not react chemically are placed in a bent tube as shown in figure. The height of the liquids above their surface of separation are

A beaker is filled with two immiscible transparent liquids of refractive indices mu_1 and mu_2 having thickness of layers d_1 and d_2 respectively. The apparent depth of the bottom of the beaker is

A point source of light S is placed at the bottom of a vessel containg a liquid of refractive index 5//3. A person is viewing the source from above the surface. There is an opaque disc of radius 1 cm floating on the surface. The centre of the disc lies vertically above the source S. The liquid from the vessel is gradually drained out through a tap. What is the maximum height of the liquid for which the source cannot at all be seen from above?

A transparent solid sphere of radius 2 cm and density rho floats in a transparent liquid of density 2rho kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8 cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10 cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3//2 and that of the liquid is 4//3.

A small ball of density rho is placed from the bottom of a tank in which a non viscous liquid of density 2 rho is filled . Find the time taken by the ball to reach the surface of liquid and maximum height reached above the bottom of container . (Size of the ball and any type of drag force acting on the ball are negligible )

A plane mirror is placed at the bottom of a tank containing a liquid of refractive index mu . P is a small object at a height h above the mirror. An observer observes P and its image in the mirror. The apparent distance between two will be

A charge Q is placed at a distance alpha/2 above the centre of a horizontal, square surface of edge a as shown in figure (30-E1). Find the flux of the electric field through the square surface.