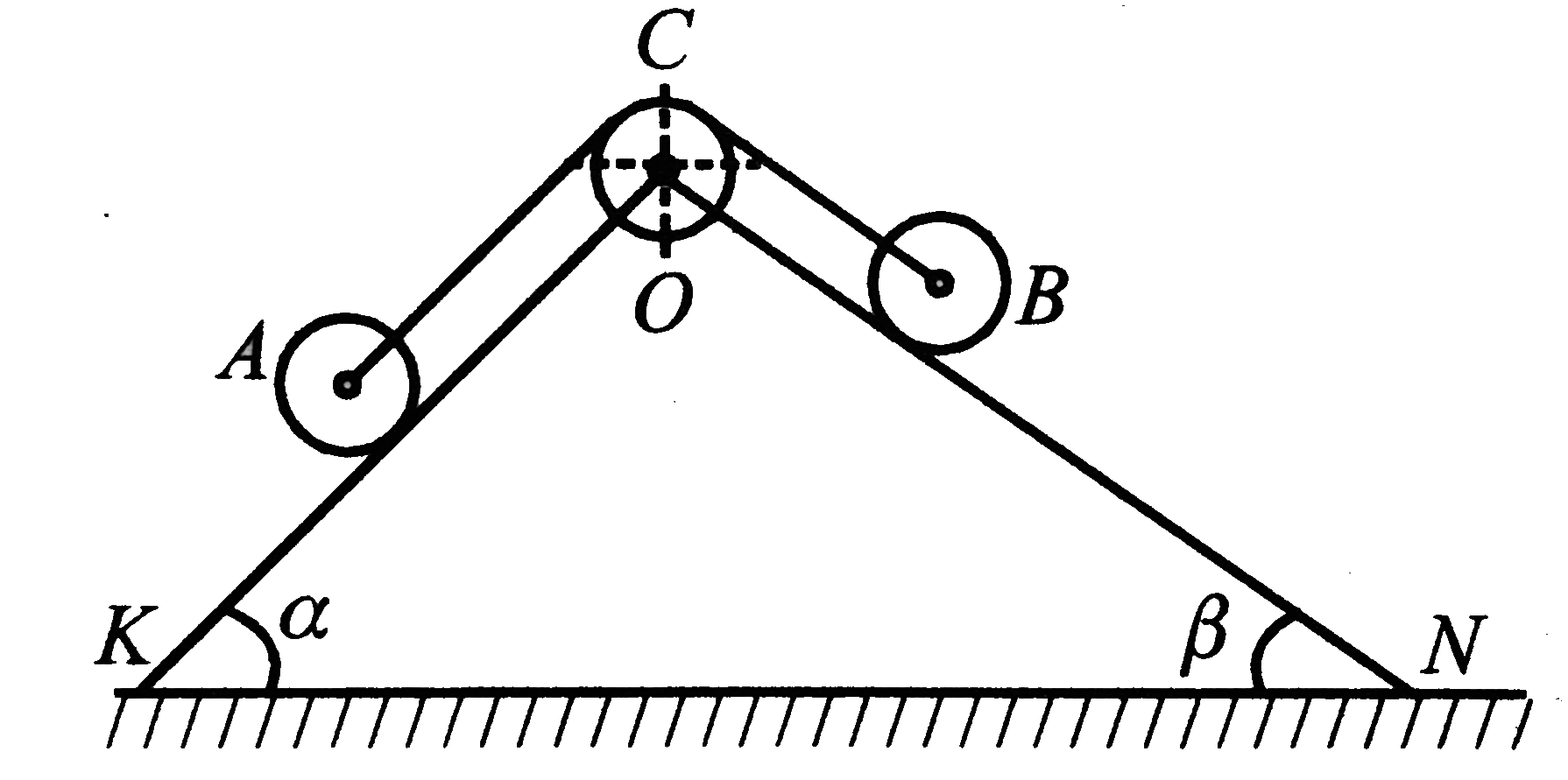
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A wheel A is connected to a second wheel B by means of in extensible s...
Text Solution
|
- A wheel is rolling on a horizontal plane. At a certain instant it has ...
Text Solution
|
- Two wheels A and B are released from rest from points X and Y respecti...
Text Solution
|
- A wheel A starts rolling up a rough inclined plane and another identic...
Text Solution
|
- An inextensible rope tied to the axle of a wheel of mass m and radius ...
Text Solution
|
- A wheel is made to roll without slipping, towards right, by pulling a ...
Text Solution
|
- A wheel of mass M and radius a and M.I. IG (about centre of mass) is s...
Text Solution
|
- A wheel moving down a perfectly frictionless inclined plane will under...
Text Solution
|
- A wheel moving down a perfectly frictionless inclined plane will under...
Text Solution
|