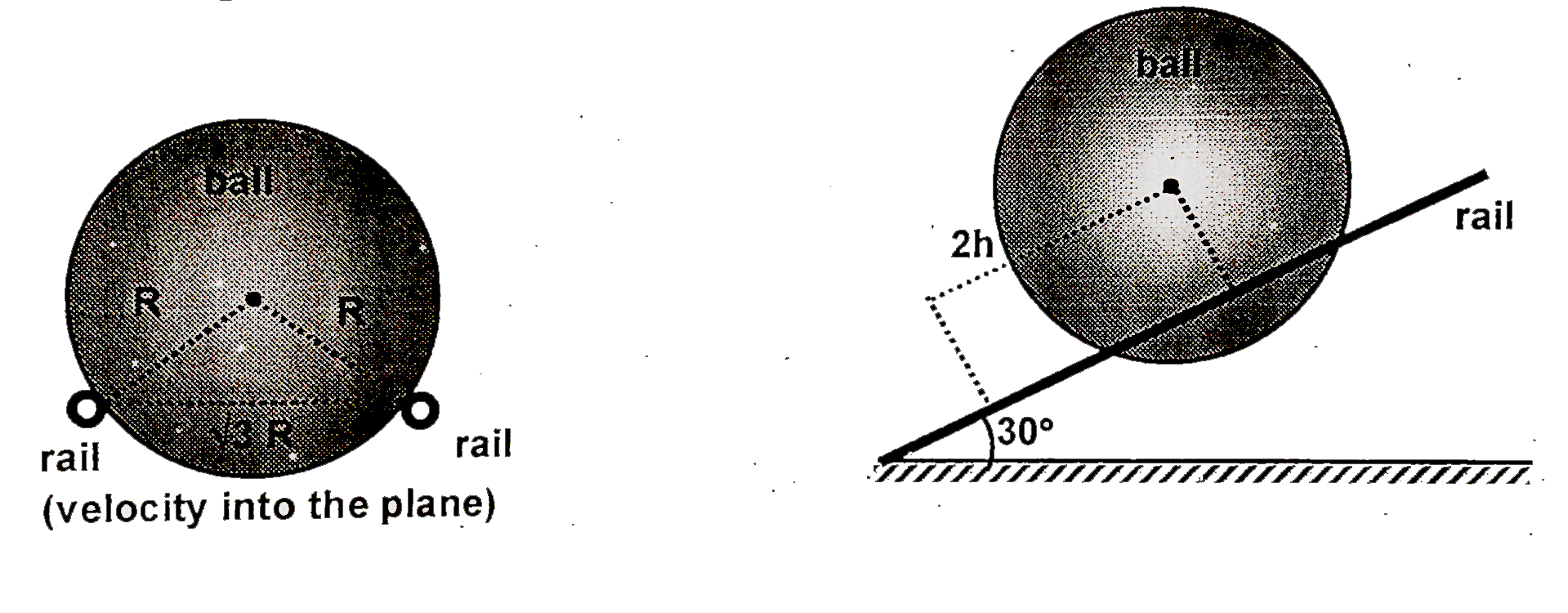A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A uniform ball of radius R rolls without slipping between the rails su...
Text Solution
|
- A ball rolls without slipping. The radius of gyration of the ball abou...
Text Solution
|
- A ball of mass m and radius r rolls inside a fixed hemispherical shell...
Text Solution
|
- A uniform ball of radius r rolls without slipping down from the top of...
Text Solution
|
- Two smooth balls A and B , each of mass m and radius R , have their ce...
Text Solution
|
- A smooth ball of mass M and radius R is lying on a smooth horizontal t...
Text Solution
|
- The cue stick hits a cue ball horizontally a distance x above the cent...
Text Solution
|
- A ball of radius r is rolling (pure rolling) on a convex stationary ci...
Text Solution
|
- In an elastic collision between two billiard balls. The variation of p...
Text Solution
|