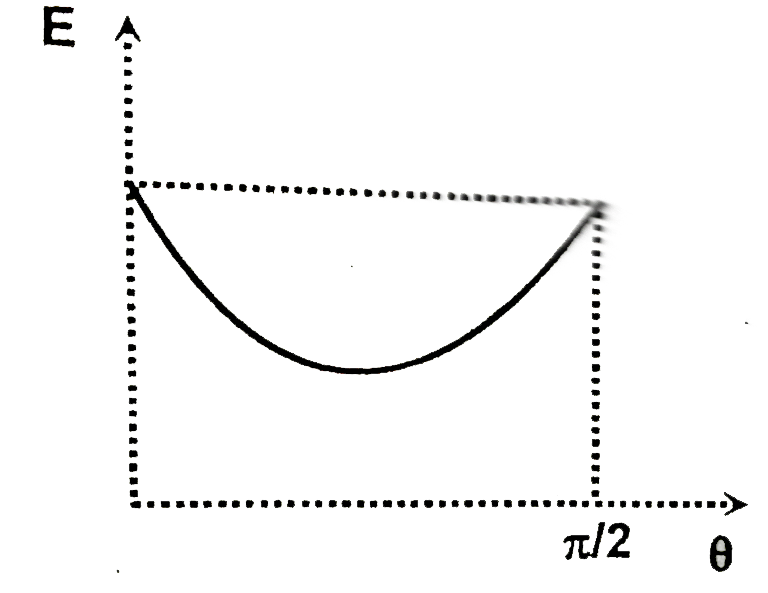
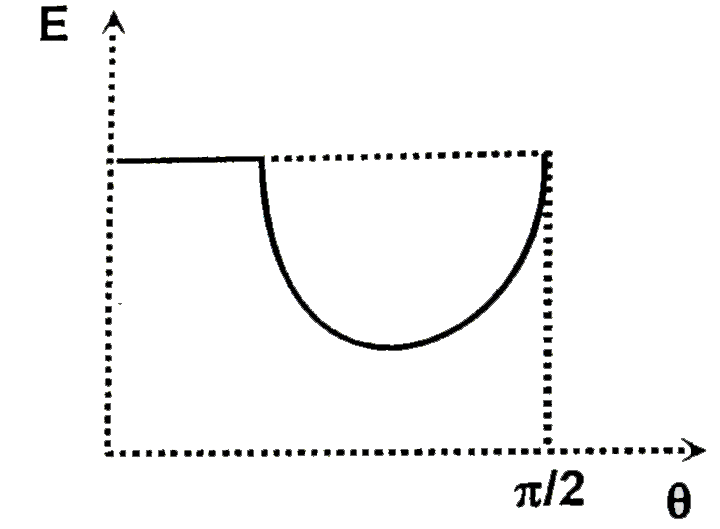
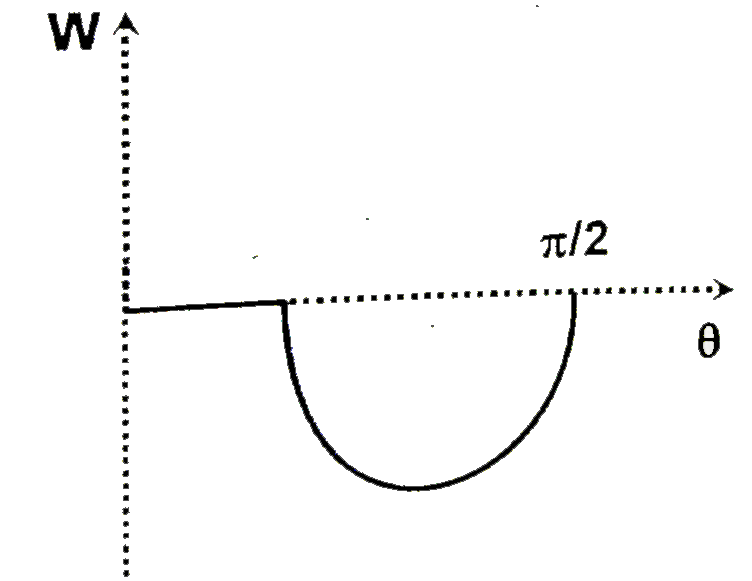
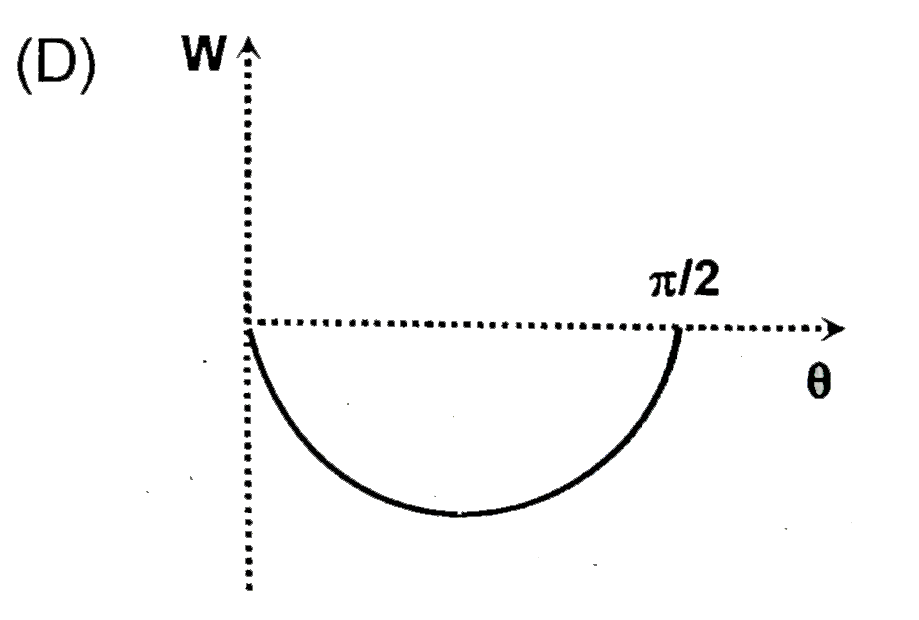
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A solid spherical ball is released from rest on an incline of inclinat...
Text Solution
|
- A hollow spherical ball is given an initial push, up an incline of inc...
Text Solution
|
- A block is at rest on an inclined plane making an angle alpha with the...
Text Solution
|
- A ball is dropped from the height h on an inclined plane of inclinatio...
Text Solution
|
- A solid sphere starts from rest at the top of an incline of height h a...
Text Solution
|
- A body is moving up an inclined plane of angle theta with an anitial k...
Text Solution
|
- A solid ball is realeased from rest down inclines of various inclinati...
Text Solution
|
- A ball is thrown upwards from the top of an incline with angle of proj...
Text Solution
|
- A body is moving up an inclined plane of angle theta with an initial k...
Text Solution
|