Home
Class 12
PHYSICS
Graphical soluton of a two body head on ...

Graphical soluton of a two body head on collision
A block `A` of mass `m` moving with a uniform velocity `v_(0)` strikes another identical block `B` kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum.

So `mv_(0)=mv_(A)mv_(B)` (`v_(A)` and `v_(B)` are the velocities of the blocks after collision)
`:. v_(0)=v_(A)+v_(B)`.........(i)
If the collision is perfectly elastic
`1/2 mv_(0)^(2)=1/2 mv_(A)^(2)+1/2 mv_(B)^(2)`
`impliesv_(0)^(2)=v_(A)^(2)+v_(B)^(2)`......(ii)
Both the above equation (i) and (ii) are plotted on `v_(A)-v_(B)` plane as shown in figure (ii). This plot can be used to find the unknowns `v_(A)` and `v_(B)`.
For example the solution of the situation in figure (i) is `v_(A)=0,v_(B)=v_(0)` (point `y` in the plot)
Because `v_(A)=v_(0), v_(B)=0` (point `x` in the plot) is not physically possible.
If the collision is perfectly inelastic, then the `v_(A)-v_(B)` plot is

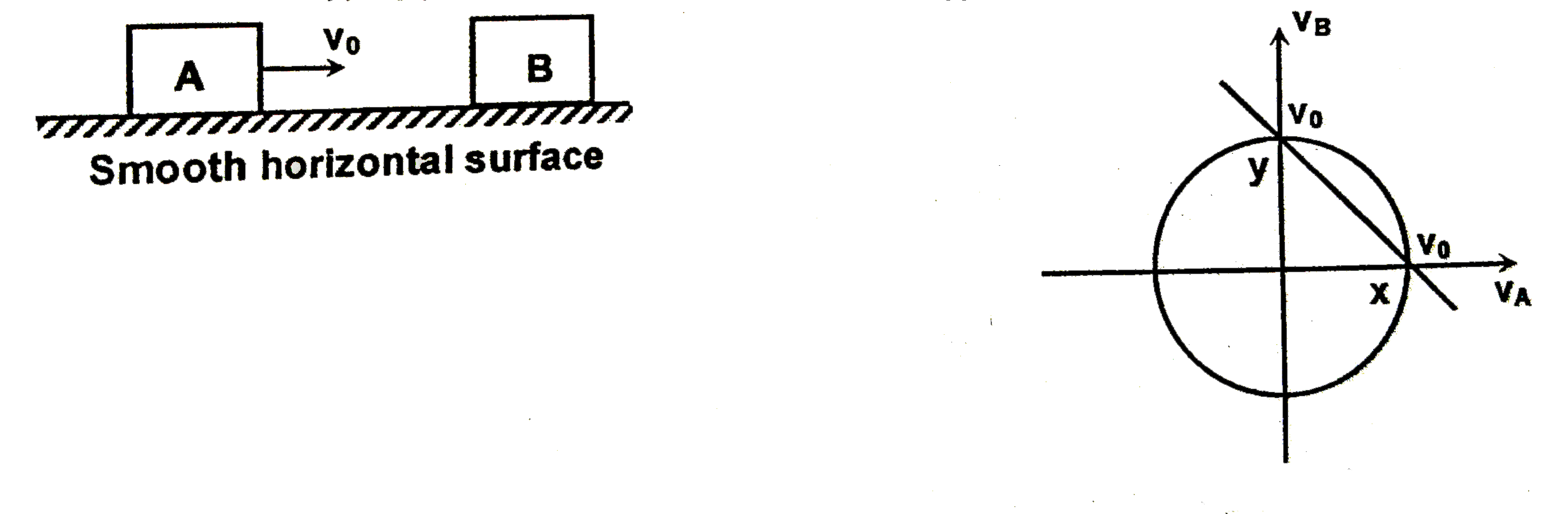
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
B
For perfectly in elastic collision both blocks have same velocity after collision.
Promotional Banner

Similar Questions

Explore conceptually related problems

Graphical soluton of a two body head on collision A block A of mass m moving with a uniform velocity v_(0) strikes another identical block B kept at rest on a horizontal smooth surface as shown in the figure (i). We can conserve linear momentum. So mv_(0)=mv_(A)mv_(B) ( v_(A) and v_(B) are the velocities of the blocks after collision) :. v_(0)=v_(A)+v_(B) .........(i) If the collision is perfectly elastic 1/2 mv_(0)^(2)=1/2 mv_(A)^(2)+1/2 mv_(B)^(2) impliesv_(0)^(2)=v_(A)^(2)+v_(B)^(2) ......(ii) Both the above equation (i) and (ii) are plotted on v_(A)-v_(B) plane as shown in figure (ii). This plot can be used to find the unknowns v_(A) and v_(B) . For example the solution of the situation in figure (i) is v_(A)=0,v_(B)=v_(0) (point y in the plot) Because v_(A)=v_(0), v_(B)=0 (point x in the plot) is not physically possible. In a situation block A is moving with velocity 2m//s an strikes another identical block B kept at rest. The v_(A)-v_(B) plot for the situation is shown. m and l are the intersection points whose v_(A), v_(B) coordinaes are given in the figure. The coefficient of restitution of the collision is

If block A is moving horizontally with velocity v_(A) , then find the velocity of block B at the instant as shown in fig.

A heavy ball of mass 2M moving with a velocity v_(0) collides elastically head on with a cradle of three identical ball each of mass M as shown in figure. Determine the velocity of each ball after collision.

A block of mass m moving with velocity v_(0) on a smooth horizontal surface hits the spring of constant k as shown. The maximum compression in spring is

A ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision

The block A is moving downward with constant velocity v_(0.) Find the velocity of the block B. When the string makes an angle theta with the horizontal

A bullet of mass m moving with velocity v strikes a suspended wooden block of mass M . If the block rises to a height h , the initial velocity of the block will be ?

Block B moves to the right with a constant velocity v_(0) . The velocity of body a relative to b is

The momentum of a particle of mass of m moving with a velocity v is p= mv. What is the rate of change of momentum ? Assume that m is constant .

A block C of mass m is moving with velocity v_(0) and collides elastically with block A of mass m and connected to another block B of mass 2m through spring constant k. What is k if x_(0) is compression of spring when velocity of A and B is same?