Home
Class 12
PHYSICS
A cylindrical massless cord of length l=...

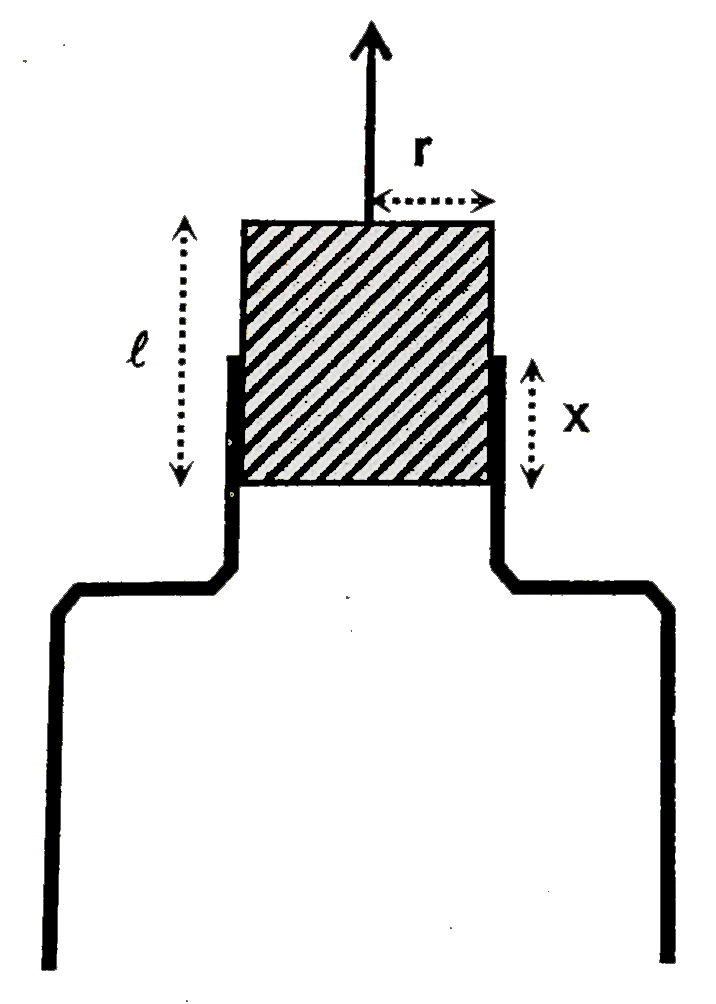
A cylindrical massless cord of length `l=10cm` and radius `r=3cm` is slowly extracted from the neck of a bottom opened bottle. If the normal pressure between the botle and un-extracted part of the cork at any instant is constant and equal to `P=(10^(5))/(pi)N//m^(2)`, find the work done (in Joule) in extracting it completely. The coefficient of friction between the cork and bottle is `mu=0.3`

Text Solution

Verified by Experts

The correct Answer is:
9
`W=int_(0)^(l) mu 2pi r x dx P`
`=pimurPl^(2)`
`=pi(0.3)(3xx10^(-2))(10^(5))/(pi)xx10^(-2)=9J`
Promotional Banner

Similar Questions

Explore conceptually related problems

Two block tied with a massless string of length 3m are placed on a rotating table as shown. The axis of rotation is 1m from 1kg mass and 2m from 2kg mass. The angular speed omega=4rad//s . Ground below 2kg block is smooth and below 1kg block is rough. (g=10m//s^(2)) (a) Find tension in the string, force of friction on 1kg block and its direction. (b) If coefficient of friction between 1kg block and groung is mu=0.8 . Find maximum angular speed so that neither of the blocksd slips. (c) If maximum tension in the string can be 100N , then maximum angular speed so that neither of the blocks slips.

A wheel of radius R=10 cm and moment of inertia I=0.05kg m^(2) is rotating about a fixed horizontal axis O with angular velocity omega_(0)=10rads^(-1) . A uniform riigid rod of mass m=3 kg and length l=50 cm is hinged at one end A such that it can rotate at end A in a vertical plane. End B of the rod is tied with a thread as shown in figure such that the rod is horizontal and is just in contact with the surface of rotating wheel. Horizontal distance between axis of rotation O of cylinder and A is equal to a = 30 cm . If the wheel stops rotating after one second after the thread has burnt, calculate coefficient of friction , mu between the rod and the surface of the wheel. (g = 10 ms^(-2))

A non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t^(3)T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be (k)/(24) . Then the value of k is

A cylinderical tank having cross sectional area ^^=0.5m^(2) is filled liquids of densities rho_(1)=900kgm^(3)&rho_(2)=600kgm^(3) to a height h=60cm as shown in the figure a small hole having area a=5cm^(2) is made in right vertical wall at a height y=20cm from the bottom calculate. (i). velocity of efflux (ii). horizontal force F to keep the cylinder in static equilibrium if it is placed on a smooth horizontal plane (iii). minimum and maximum value of F to keep the cylinder at rest. The coefficient of friction between cylinder and the plane is mu=0.1 (iv). velocity of the top most layer of the liquid column and also the velocity of the boundary separating the two liquids.

A cylindrical tank having cross-sectional area A = 0.5 m^(2) is filled with two liquids of density rho_(1)=900 kg m^(-3) and rho_(2)=600 kgm^(-3) , to a height h=60cm each as shown in the figure. A small hole having area a=5cm^(2) is made in right vertical wall at a height y = 20 cm from the bottom. A horizontal force F is applied on the tank to keep it in static equilibrium. The tank is lying on a horizontal surface. Neglect mass of the cylindrical tank in comparison to mass of the liquids ( ake g = 10 ms^(-2) ). (i) horizontal force F to keep the cylinder in static equilibrium, if it is placed on a smooth horizontal plane and (ii) minimum and maximum values of F to keep the cylinder in static equilibrium, if coefficient of friction between the cylinder and the plane is µ = 0.01. (g = 10 ms –2 )

A body of mass 0.3kg is taken up an inclined plane of length 10m and height 5m, and then allowed to slide down to the bottom again. The coefficient of friction between the body and the plane is 0.15 . What is the (a) work done by the gravitational force over the round trip. (b) work done by the applied force over the upward journey (c ) work done by frictional force over the round trip. (d) kinetic energy of the body at the end of the trip. How is the answer (d) related to the first three answers ? m=0.3kg , OA=10m , BA=5m

A large slab of mass 5kg lies on a smooth horizontal surface, with a block of mass 4kg lying on the top of it. The coefficient of friction between the block and the slab is 0.25 . If the block is pulled horizontally by a force of F =6N , the work done by the force of friction on the slab, between the instants t=2s and t=3s , is (g=10ms^-2)

A semicircular track of radius R=62.5cm is cut in a block. Mass of block having track, is M=1kg and rests over a smooth horizontal floor. A cylinder of radius r=10 cm and mass m=0.5kg is hanging by thread such that axes of cylinder and track are in same level and surface of cylinder is in contact with the track as shown in figure When the thread is burnt, cylinder starts to move down the track. Sufficient friction exists between surface of cylinder and track, so that cylinder does not slip. Calculate velocity of the block when it reaches bottom of the track. Also find force applied by block on the floor at that moment. (g=10m//s^(2))

AB is a quarter of smooth circular track of radius R=6m . A particle P of mass 0.5kg moves along the track from A to B under the action of the following forces. a. A force F_1 directed always towards the point B, its magnitude is constant and is equal to 20N . b. A force F_2 directed along the instantaneous tangent to the circular track, its magnitude is (15-10S)N , where S is the distance travelled in metre. c. A horizontal force of magnitude 30N . Find the work done by forces mentioned in (a), (b) and (c)

A cylindrical rod of length 50cm and cross sectional area 1cm^(2) is fitted between a large ice chamber at 0^(@)C and an evacuated chamber maintained at 27^(@)C as shown in figure. Only small protions of the rod are insid ethe chamber and the rest is thermally insulated from the surrounding. The cross section going inti the evacuted chamber is blackened so that it completely absorbe any radiation falling on it. The temperatuere of the blackened end is 17^(@)C when steady state is reachhed. Stefan constant sigma=6xx10^(-s)Wm^(-2)K^(-4) . Find the thermal conductivity of the material of the rod.