Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
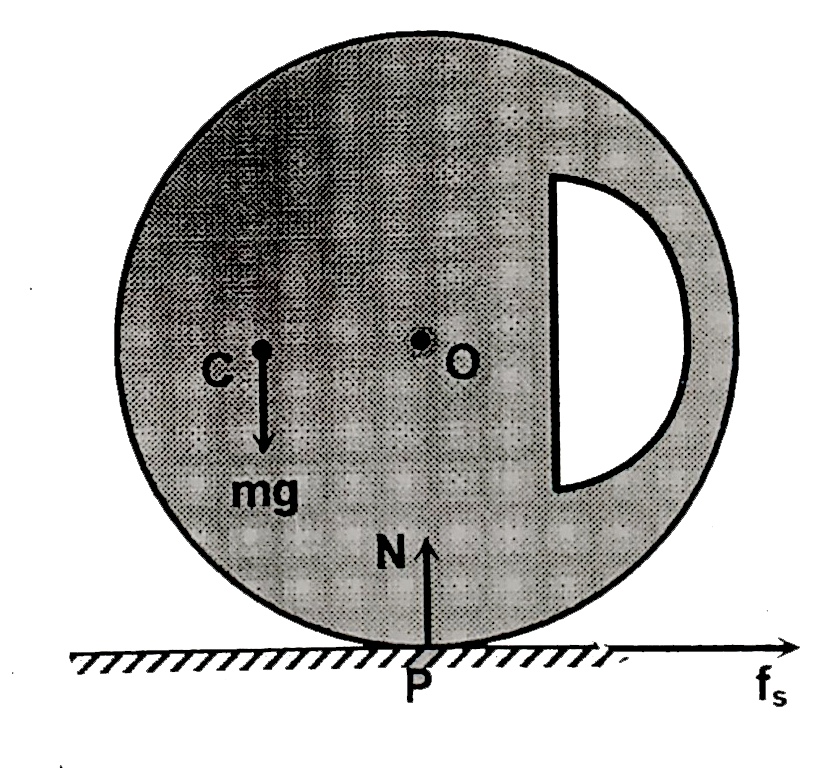
- A disc shaped body (having a hole shown in the figure) of mass m=10kg ...
Text Solution
|
- A small hole is made in a disc of mass M and radius R at a distance R/...
Text Solution
|
- A disc of mass m and radius r placed on a routh horizontal surface. A ...
Text Solution
|
- A point mass m collides with a disc of mass m and radius R resting on ...
Text Solution
|
- A thin disc of mass 9M and radius R from which a disc of radius R/3 is...
Text Solution
|
- From a circular disc of radius R and mass 9M, a small disc of radius R...
Text Solution
|
- A disc has mass 9 m. A hole of radius R/3 is cut from it as shown in t...
Text Solution
|
- A disc of mass M and radius R is rolling with angular speed w on horiz...
Text Solution
|
- Find the radius of gyration of a disc of mass M and radius R rotating ...
Text Solution
|