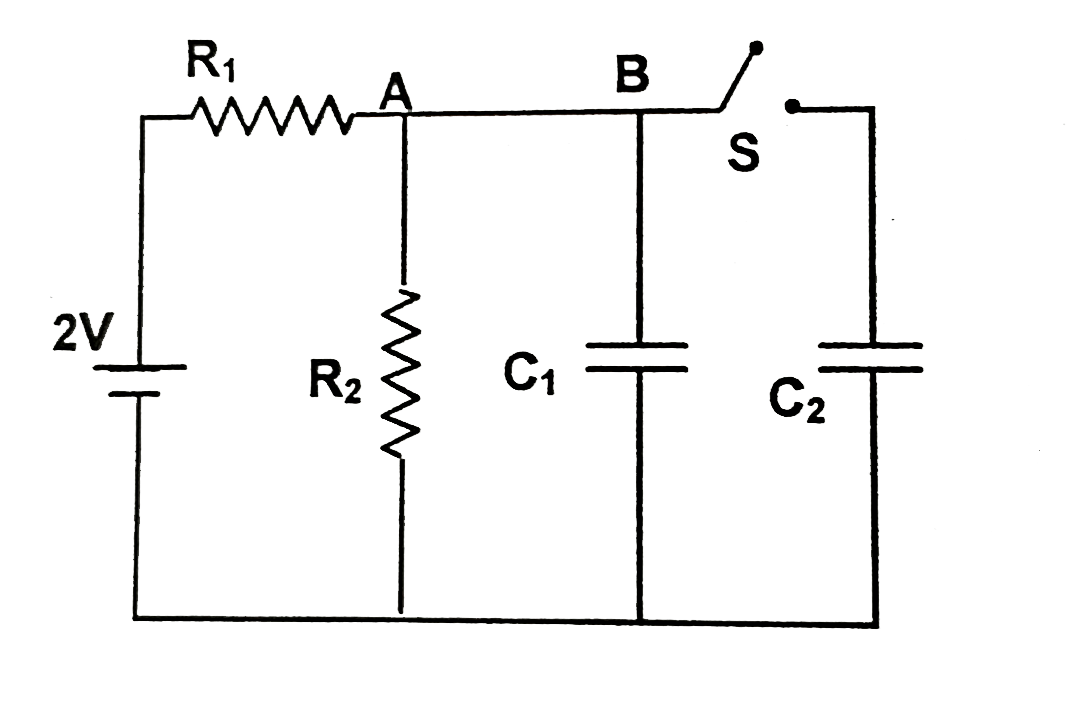
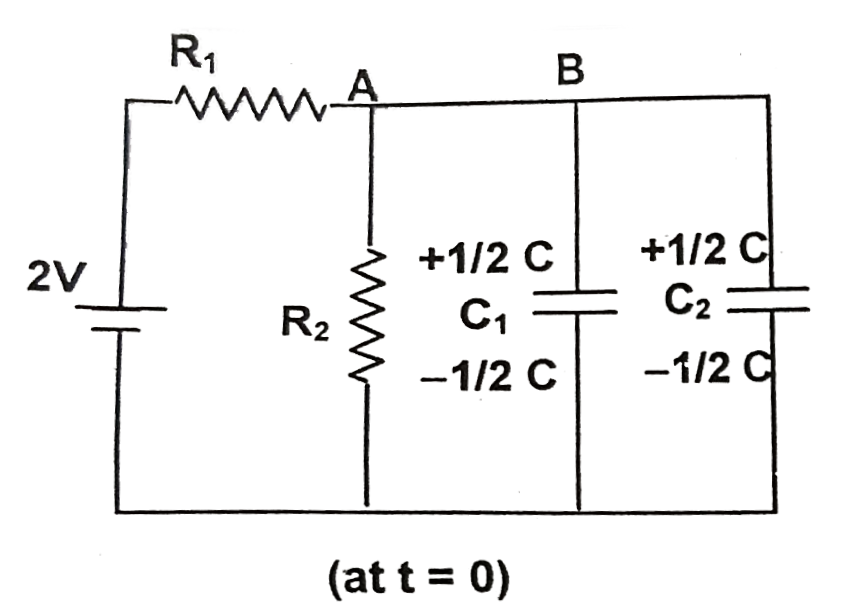
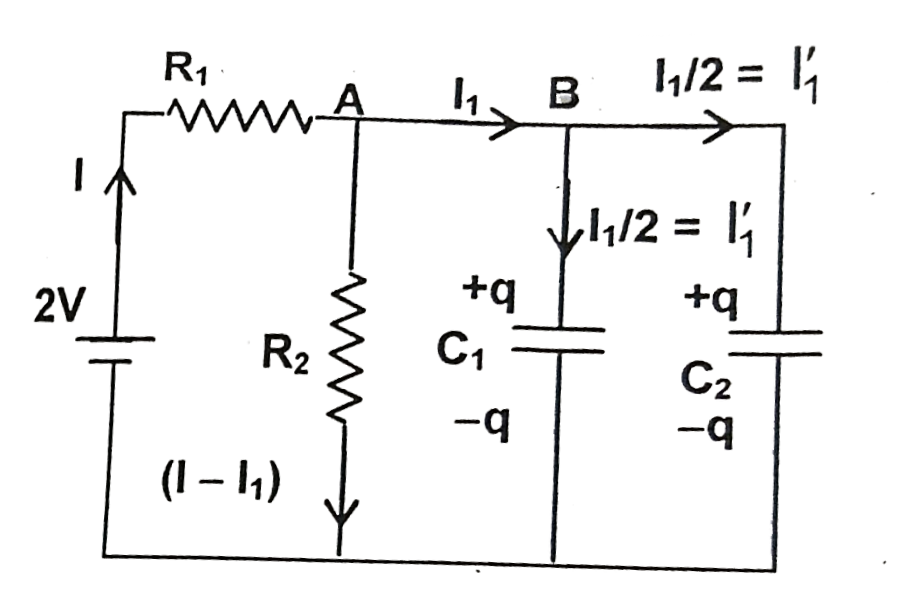A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Initially the switch 'S' is open for a ling time. Now the switch 'S' i...
Text Solution
|
- In the circuit shows in Fig E = 15 V, R(1) = 1Omega, R(2) = 1 Omega, R...
Text Solution
|
- The figure below shown a battery with emf 15 V in a circuit with R(1) ...
Text Solution
|
- An inductor of inductance L = 400 mH and resistors of resistance R(1) ...
Text Solution
|
- In the figure shown C(1)=1F, C(2)=2F and L=5H . Initially C(1) is char...
Text Solution
|
- In the figure shown C(1)=1F, C(2)=2F and L=5H. Initially C(1) is charg...
Text Solution
|
- As shown in diagram initial charge on capacitor is zreo . Now switch S...
Text Solution
|
- In the following circuit, the switch S is closed at t = 0. The charge ...
Text Solution
|
- एक प्रेरक, जिसका प्रेरकत्व L= 400 mH मिली होगी है तथा दो प्रतिरोधक जिन...
Text Solution
|