Home
Class 12
PHYSICS
A resitance R=1kOmega connected to a con...

A resitance `R=1kOmega` connected to a conducting rod `PQ` that can slide on a conducting circular ring of radius `2m` with center at `P`. A constant uniform magnetic field 10 Tesla exist as shown in figure. At `t=0`, switch `'S'` is closed and simulaneously an external torque is applied on the rod so that it rotates with constant angular velocity `20"rad"//"sec"`. The magnitude of power delivered by external is `20K` Watt. Find the value of `K`. (Neglect the gravity, friction and self inductance of circular loop)

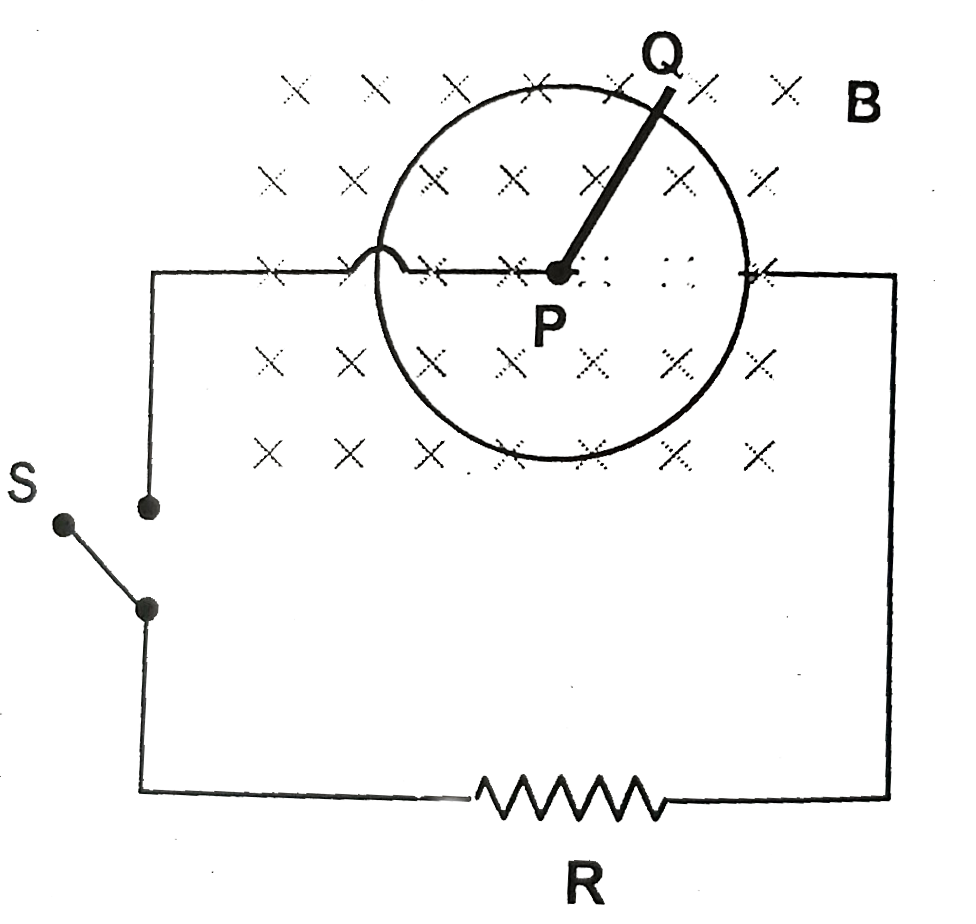
Text Solution

Verified by Experts

The correct Answer is:
8
Induced emf `=(Bomegal^(2))/2`, current `i_(0)=(Bomegal^(2))/(2R)`
Torque about `P=tau=int(idx)B.x=(iBl^(2))/2`
`=((Bomegal^(2))/(2R))((Bl^(2))/2)=8`
So, power `P= tau.vecomega=160` Watt
Alternate Solution
Power `=` Heat loss in resistance `=Ri_(1)^(2)=(B^(2)omega^(2)l^(4))/(4R)=160` Watt
Promotional Banner

Similar Questions

Explore conceptually related problems

The circuit shows a resistance, R=0.01Omega and inductance L=3mH connected to a conducting rod PQ of length l=1m which can slide on a perfectly conducting circular arc of radius l with its center at P. Assume that friction and gravity are absent and a constant uniform magnetic field b=0.1T exists as shown in the figure. At t=0, the circuit is seitched on a simultaneously an external torque is applied on the rod so that it rotates about P with a constant angular velocity omega =2 rad//sec . Find the magnitude of this torque (inN-m) at t=(0.3In 2) second.

The diagram shows a circuit having a coil of resistance R = 2.5 (Omega) and inductance L connected to a conducting rod PQ which can slide on perfectly conducting circular ring of radius 10 cm with its centre at 'P'. Assume that friction and gravity are absent and a constant uniform magnetic field of 5 T exist as shown in Fig. At t = 0, the circuit is switched on and simultaneously a time varying external torque is applied on the rod so that it rotates about P with a constant angular velocity 40 rad//s . Find magnitude of this torque (in milli Nm) when current reaches half of its maximum value. Neglect the self-inductance of the loop formed by the circuit.

Figure shows a circuit having a coil of resistance R = 2.5 Omega and inductance L connected to a conducting rod of radius 10 cm with its center at P . Assume that friction and gravity are absent and a constant uniform magnatic field of 5 T exists as shown in figure. At t = 0 , the circuit is switched on and simultaneously a time-varying external torque is applied on the rod so that it rotates about P with a constant angular velocity 40 rad s^(-1) . Find the magnitude of this torque (in mNm ) when current reaches half of its maximum value. Neglect the self inductance of the loop formed by the circuit.

In the above question find the force required to move the rod with constant velocity v , and also find the power delivered by the external agent.

A semi circular conducting ring acb of radius R moves with constant speed v in a plane perpendicular to uniform magnetic field B as shown in figure. Identify the correct statement.

Calculate the instantenous power of a wheel rotating with an angular velocity of 20"rad"//s , when a torque of 10Nm is applied to it.

Calculate the instantenous power of a wheel rotating with an angular velocity of 20"rad"//s , when a torque of 10Nm is applied to it.

AB is a resistanceless conducting rod which forms a diameter of a conducting ring of radius r rotating in a uniform magnetic field B as shown in figure. The resistance R_(1) and R_(2) do not rotate. Then the current through the resistor R_(1) is

AB is a resistanceless conducting rod which forms a diameter of a conducting ring of radius r rotating in a uniform magnetic field B as shown in figure. The resistance R_(1) and R_(2) do not rotate. Then the current through the resistor R_(1) is

A conducting rod of length l is rotating with constant angular velocity omega about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?