Home
Class 12
MATHS
DeltaABC is equilateral triangle of side...

`DeltaABC` is equilateral triangle of side a. P lies on AB such that A is midpoint of PB. If `r_(1)` is inradius of PAC and `r_(2)` is ex radius of PBC opposite to P, then `r_(1) + r_(2) =`

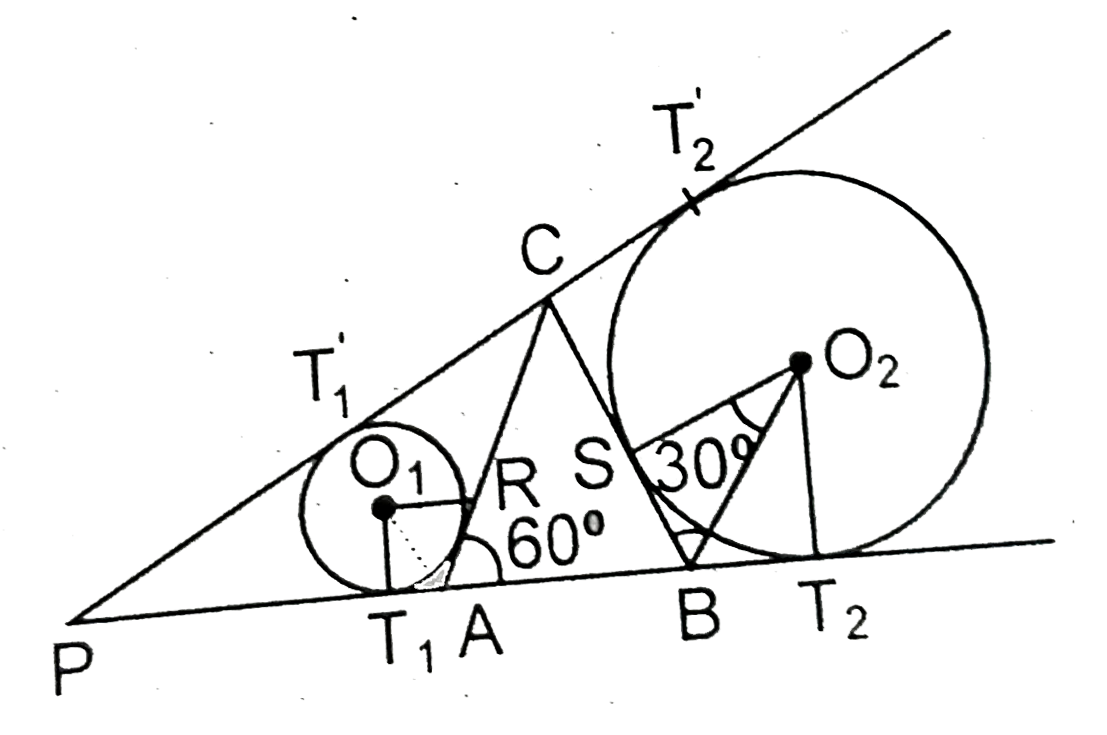
Text Solution

Verified by Experts

The correct Answer is:
`00000.50`
`/_T_(1)O_(1)R=60^(@)` and `/_AO_(1)R=0^(@)`
similarly `/_BO_(2)S=30^(@)`
`T_(1)T_(2)=T_(1)A+AB+BT_(1)=RA+RB+SB`
`=r_(1) tan 30^(@)+a+r_(2)tan30^(@)=(r_(1)+r_(2))/(sqrt(3))+a`
and `T_(1)^(')T_(2)^(')=T_(1)^(')C+T_(2)^(')C=a-RA+a-BS=2a-(r_(1)+r_(2))/(sqrt(3))`
Since common external tangents are equal `T_(1)T_(2)=T_(1)^(')T_(2)^(')`
`implies r_(1)+r_(2)=(sqrt(3)a)/2`
Promotional Banner

Similar Questions

Explore conceptually related problems

In the given figure DeltaABC is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of DeltaABC , r_1 as the radius of incircle DeltaPAC and r_2 as the ex-radius of DeltaPBC with respect to side BC. Then r_1 + r_2 is equal to

Let ABC be an isosceles triangle with base BC. If r is the radius of the circle inscribsed in DeltaABC and r_(1) is the radius of the circle ecribed opposite to the angle A, then the product r_(1) r can be equal to (where R is the radius of the circumcircle of DeltaABC )

A B C is an equilateral triangle of side 4c mdot If R ,r and h are the circumradius, inradius, and altitude, respectively, then (R+r)/h is equal to

In triangle ABC, let angle C = pi//2 . If r is the inradius and R is circumradius of the triangle, then 2(r + R) is equal to

In an equilateral triangle with usual notations the value of (27r^(2)R)/(r_(1)r_(2)r_(3)) is equal to

A B C is an equilateral triangle of side 4c mdot If R , r, a n d,h are the circumradius, inradius, and altitude, respectively, then (R+r)/h is equal to (a) 4 (b) 2 (c) 1 (d) 3

In a DeltaABC, r_(1) + r_(2) + r_(3) -r =

In a triangle ABC , if 2R + r = r_(1) , then

In an equilateral triangle show that the in-radius and the circum-radius are connected by r =R/2.

In a triangle ABC if sides a = 13, b =14 and c = 15, then reciprocals of r_(1),r_(2),r_(3) are in the ratio