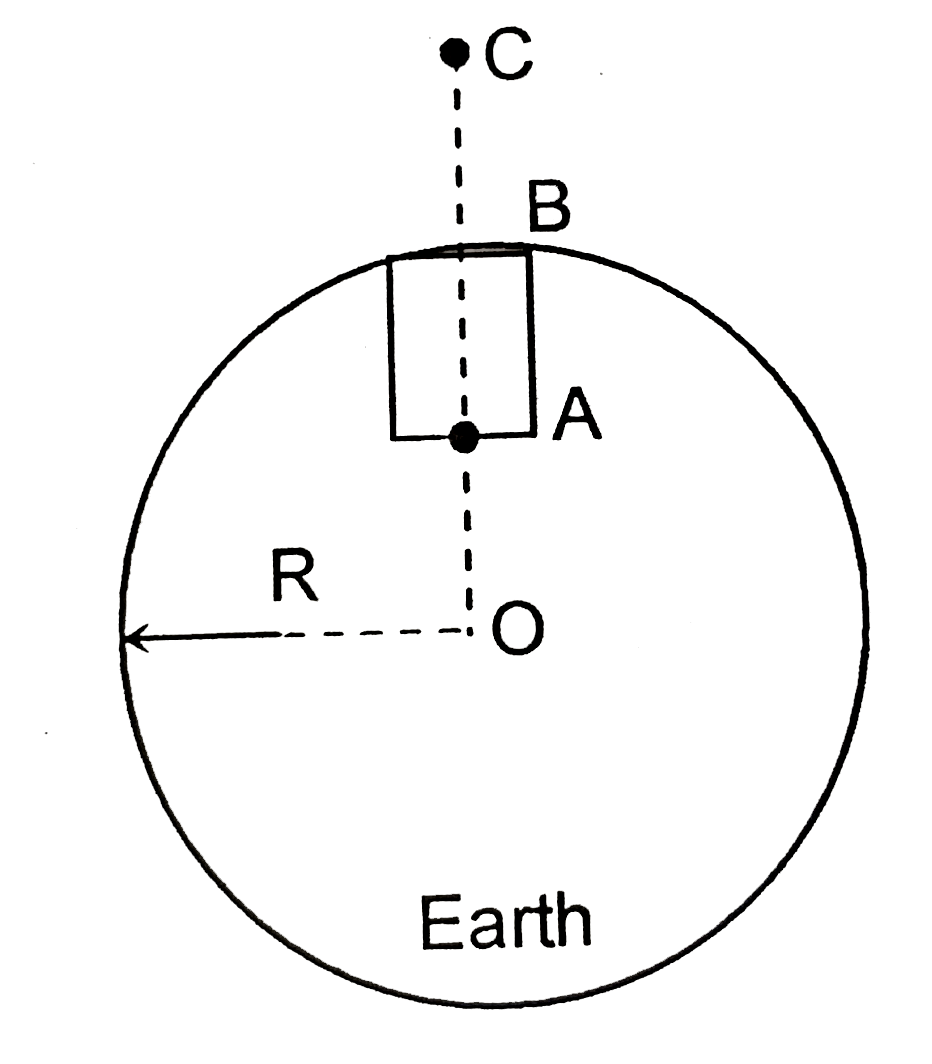
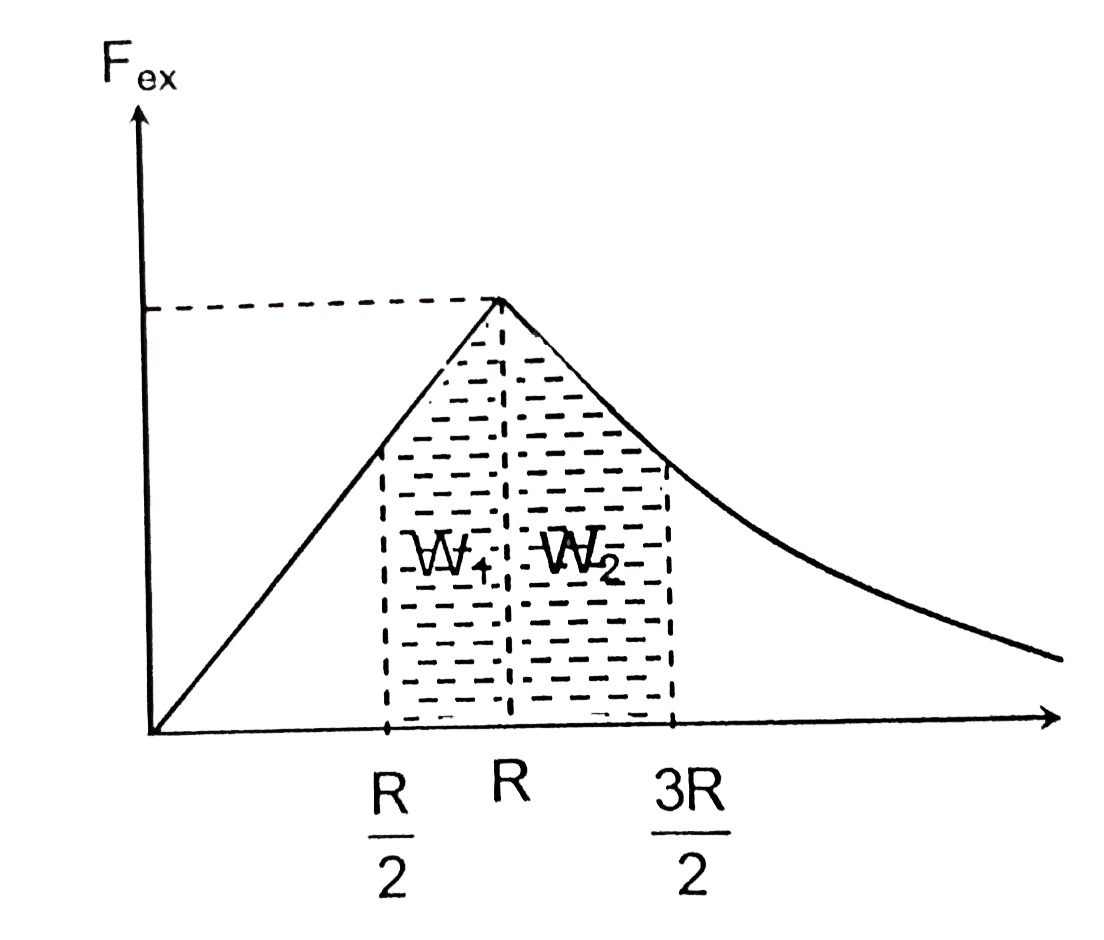
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- First an object is slowly lifted from the bottom(point -A) of a shaft ...
Text Solution
|
- Let z1=a+i b and z2=c+i d are two complex number such that |z1|=|z2|...
Text Solution
|
- If W(1) W(2) and W(3) represent the work done in moving a particle fro...
Text Solution
|
- Let the minimum external work done in shifting a particle from centre ...
Text Solution
|
- In the following diagram the work done in moving a point charge from p...
Text Solution
|
- Apparent depth for point object x in all three cases are H(1),H(2) & H...
Text Solution
|
- The work done in slowly lifting a body from earth's surface to a heigh...
Text Solution
|
- दो प्रकाश संवेदी धातुओं पर, जिनके कार्यफलन क्रमशः W(1) और W(2) है, परा...
Text Solution
|
- If the acceleration due to gravity at the surface of the earth is g, t...
Text Solution
|