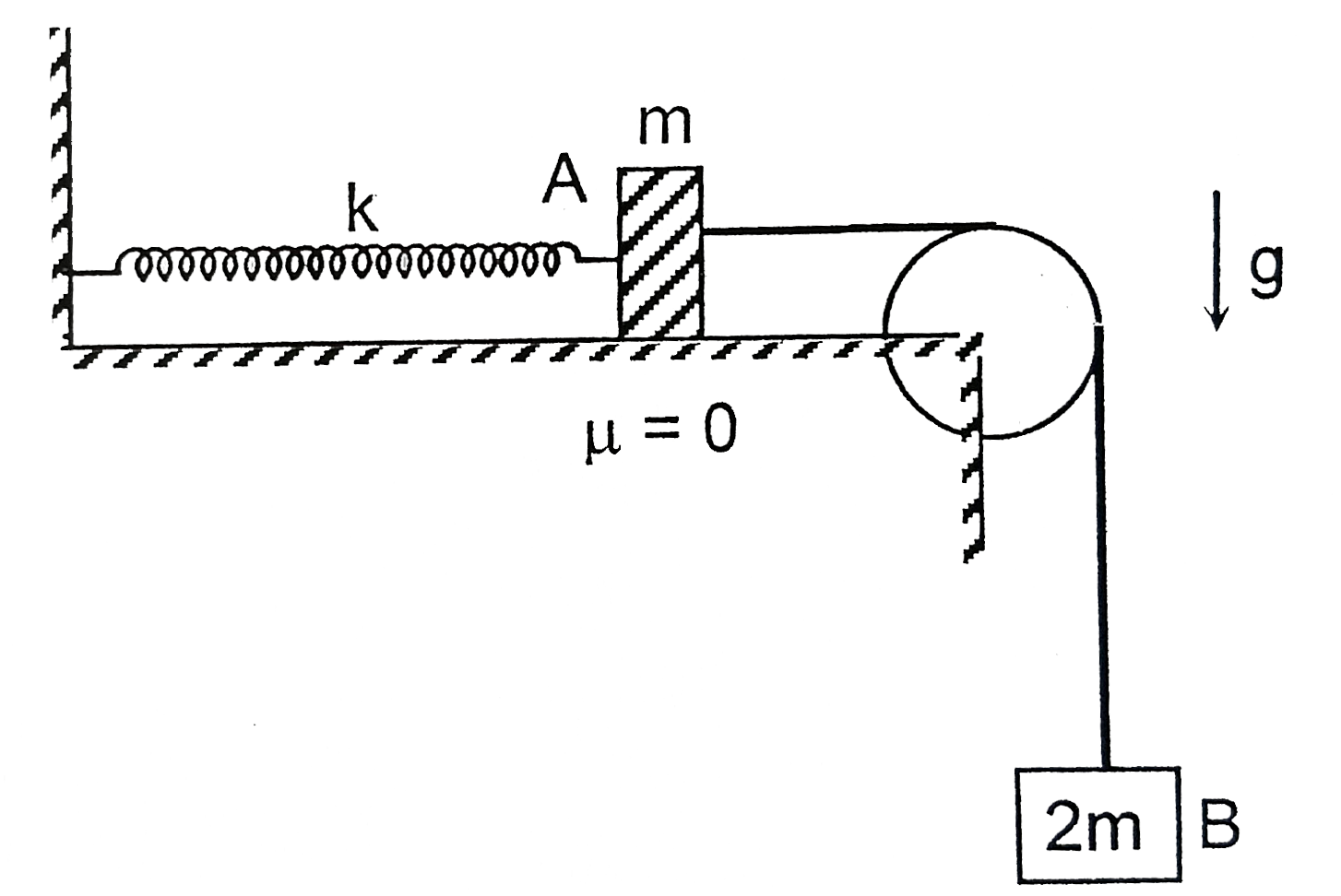
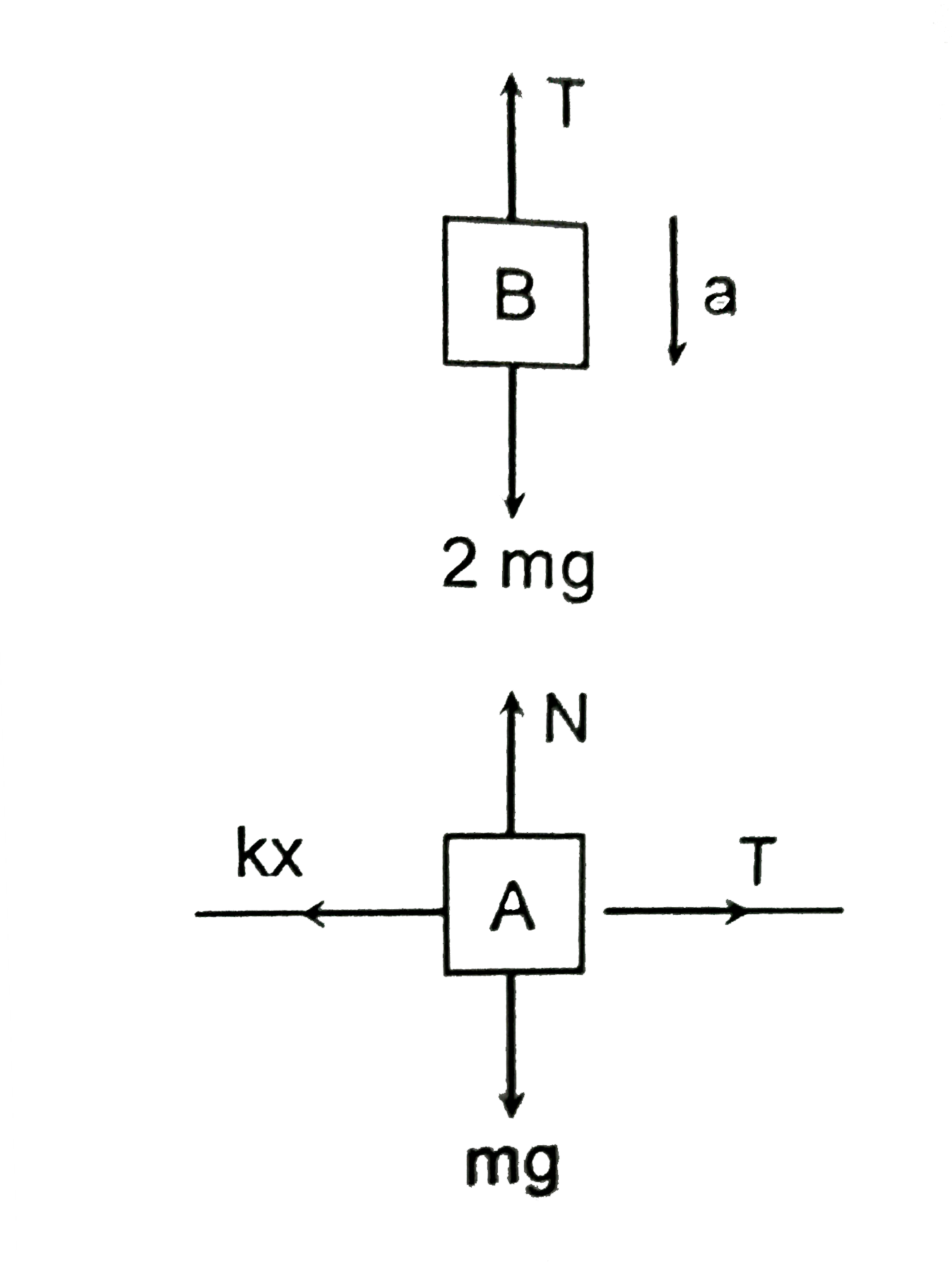
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- All the surfaces are frictionless and system is released from test whe...
Text Solution
|
- A system of wedge and block as shown in figure, is released with the s...
Text Solution
|
- A vertical spring is fixed to one of its end and a massless plank plan...
Text Solution
|
- In an ideal pulley particle system, mass m2 is connected with a vertic...
Text Solution
|
- In the above situation all surface are frictionless system is released...
Text Solution
|
- A disc of mass m is connected with an ideal spring of stiffness k. If ...
Text Solution
|
- An ideal string pulley system is shown in the figure and system is rel...
Text Solution
|
- In the shown figure, the spring and string is ideal. The spring the st...
Text Solution
|
- A block suspended from a spring is released when the spring is unstret...
Text Solution
|