Home
Class 12
PHYSICS
A large cylindrical container with open ...

A large cylindrical container with open top contains a liquid upto height `(2H=8m)` and whose density varies as shown in the figure. Atmospheric pressure is 1 atm `(=10^(5)N//m^(2))`
Find the pressure at botom of cylindrical container in atm.
(given `rho_(0)=10^(3)Kg//m^(2),` and `g=10m//s^(2)`)

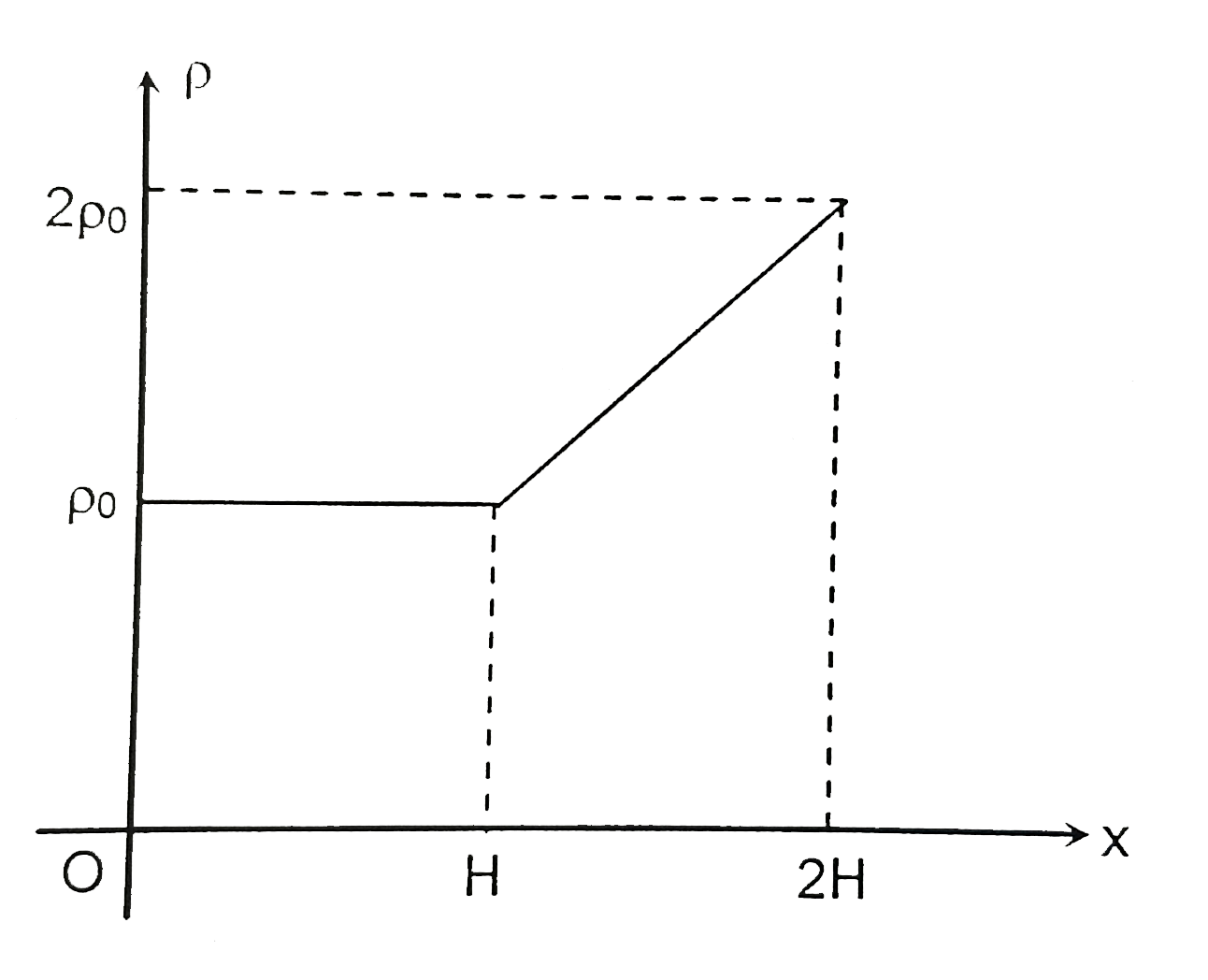
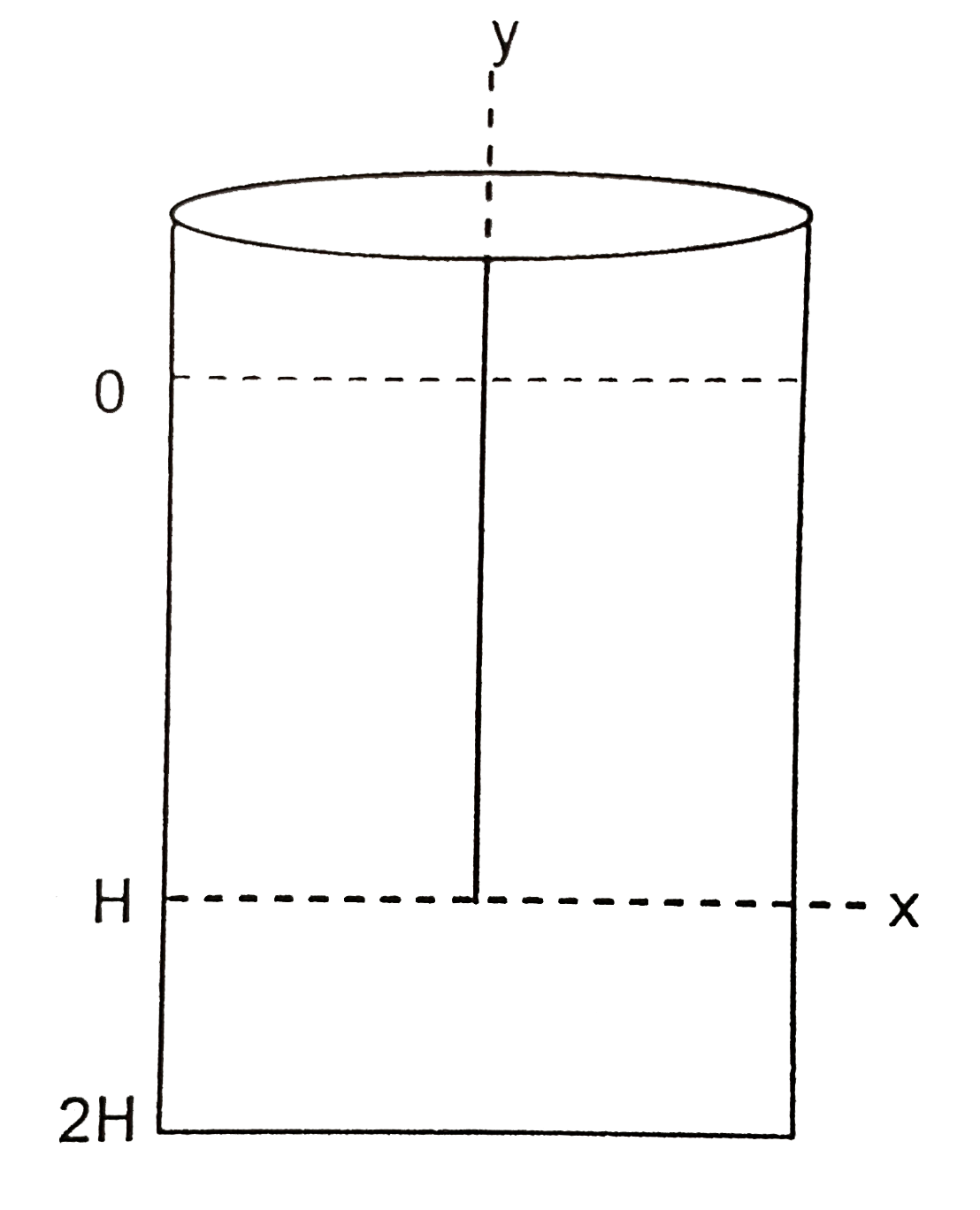
Text Solution

Verified by Experts

The correct Answer is:
2
We have to calculate the partial pressure, generated due the liquid of variable density
`rho=(rho_(0))/Hy+rho_(0)`
`W=` weight of liquid column above the point `A`
`impliesW=int_(y)^(H)Srhogdy=gSrho_(0) int_(y)^(H)(1+y/H)dy`
`=gsrho_(0)[(H-y)+(H^(2)-y^(2))/(2H)]=(Srho_(0)(H-y)(3H-y)g)/(2H)`
`P_(1)=` Patial pressure at interface `(y=0)` due to liquid with variable density `=W/S|_(y=0)`
`=(3rho_(0)gH)/2`
`Pimplies` Pressure at bottom `=P_(0)+P_(1)+rho_(0)gH=rho_(0)+(5rho_(0)gH)/2`
`=10^(5)+(5xx10^(3)xx10xx4)/2=2xx10^(5)=2` atm
Promotional Banner

Similar Questions

Explore conceptually related problems

Water (rho=10^(3)kg//m^(3)) is filled in tube AB as shown in figure. (omega=10 rad//s) . Tube is open at end A. Atmospheric pressure is p_(0)=10^(5)N//m^(2) . Find absolute pressure at end B . .

A container (see figure) contains a liquid upto a height h. The density of the liquid is The gauge pressure at point P is (rho gh )/(x ) . Find the value of x

A cylindrical vessel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P_0 , find the pressure of the liquid just below the piston. ,

A container filled with a liquid of density 4p as shown in the figure. The velocity efflux through orifice is ( rho is density of water and g = 10 ms^(-2) )

What is the absolute pressure on a swimmer 10 m below the surface of a lake? Take atmospheric pressure 1xx10^(5)N//m^(2)

A cylindrical vessel of a very large cross sectional area is containing two immiscible liquids of density rho_(1)=600kg//m^(3) and rho_(2)=1200kg//m^(3) as shown in the figure. A small hole having cross sectional area 5cm^(2) is made in right side vertical wall as shown. Take atmospheric pressure as p_(0)=10^(5)N//m^(2), g=10m//s^(2) . For this situation mark out the correct statement (s). Take cross sectional area of the cylindrical vessel as 1000cm^(2) . Neglect the mass of the vessel.

A square plate of side 10 m is placed horizontally 1 m below the surface of water. The atmospheric pressure is 1.013xx10^(5)Nm^(-2) . Calculate the total thrust on the plate. (Density of water rho=10^(3)kg m^(-3), g=9.8ms^(-2))

What is the pressure in an ocean at a depth of 1000 m, if the density of water is 1.024xx 10^(3) (kg)/m^(3) . Atmospheric pressure P. = 1.01 xx 10^(5) Pa.

The pressure at a point in water is 10 N//m^(2) . The depth below this point where the pressure becomes double is (Given density of water = 10^(3) kg m^(-3) , g = 10 m s^(-2) )

A siphon tube is discharging a liquid of density 900(kg)/(m^(3)) as shown in figure. (P_(0)=1.01xx10^(5) N//m^(2)) Pressure at point B is