Home
Class 12
MATHS
Let A(z(1)), B(z(2)), C(z(3) and D(z(4))...

Let `A(z_(1)), B(z_(2)), C(z_(3)` and `D(z_(4))` be the vertices of a trepezium in an Argand plane such that `AB||CD` Let `|z_(1)-z_(2)|=4, |z_(3),z_(4)|=10` and the diagonals `AC` and `BD` intersects at `P`. It is given that `Arg((z_(4)-z_(2))/(z_(3)-z_(1)))=(pi)/2` and `Arg((z_(3)-z_(2))/(z_(4)-z_(1)))=(pi)/4`
Which of the following option(s) is/are incorrect?

A

Value of `|CP-DP|` is equal to `10/(sqrt(21))`

B

`PB:PD=2:5`

C

`PC:AC=5:7`

D

`PC:AC=2:3`

Text Solution

Verified by Experts

The correct Answer is:
D
`DeltaABP` and `DeltaCDP` are similar if `AP=2x`
`BP=2y` then `CP=5x, DP=5y`
Area of trapezium `ABCD=49/2xy`
`tan alpha=(2x)/(5y), tan beta =(2y)/(2x)` also `alpha+beta=45^(@)`
`impliesxy=10/21(x^(2)+y^(2))`
Also `AB^(2)=AP^(2)+BP^(2)impliesx^(2)+y^(2)=4impliesxy=40/21`
`Ar(DeltaPCD)=5xy`
Promotional Banner

Similar Questions

Explore conceptually related problems

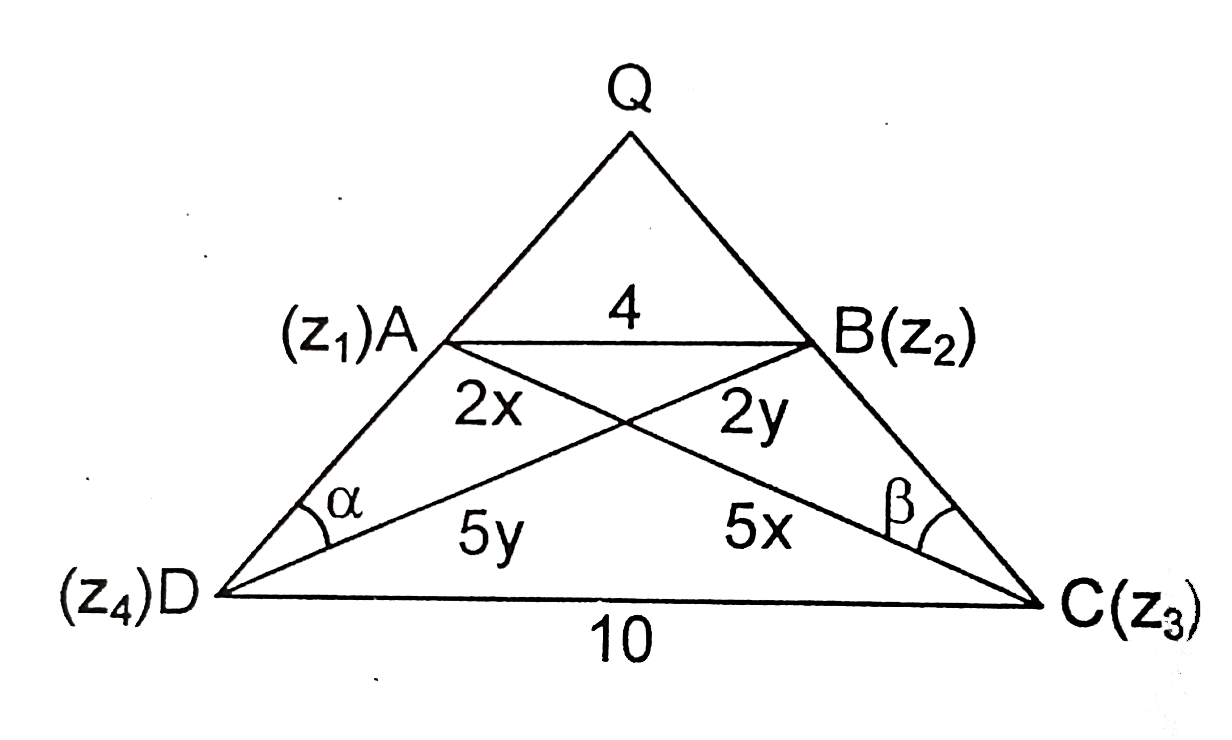
Let A(z_(1)), B(z_(2)), C(z_(3) and D(z_(4)) be the vertices of a trepezium in an Argand plane such that AB||CD Let |z_(1)-z_(2)|=4, |z_(3),z_(4)|=10 and the diagonals AC and BD intersects at P . It is given that Arg((z_(4)-z_(2))/(z_(3)-z_(1)))=(pi)/2 and Arg((z_(3)-z_(2))/(z_(4)-z_(1)))=(pi)/4 Which of the following option(s) is/are correct?

Let A(z_(1)),B(z_(2)),C(z_(3)) be the vertices of an equilateral triangle ABC in the Argand plane, then the number (z_(2)-z_(3))/(2z_(1)-z_(2)-z_(3)) , is

If z_(1), z_(2) and z_(3) are the vertices of a triangle in the argand plane such that |z_(1)-z_(2)|=|z_(1)-z_(3)| , then |arg((2z_(1)-z_(2)-z_(3))/(z_(3)-z_(2)))| is

If z_(1),z_(2),z_(3) are the vertices of an equilational triangle ABC such that |z_(1)-i|=|z_(2)- i| = |z_(3)-i|, then |z_(1)+z_(2)+z_(3)| equals to

If A(z_(1)) , B(z_(2)) , C(z_(3)) are vertices of a triangle such that z_(3)=(z_(2)-iz_(1))/(1-i) and |z_(1)|=3 , |z_(2)|=4 and |z_(2)+iz_(1)|=|z_(1)|+|z_(2)| , then area of triangle ABC is

If A(z_(1)),B(z_(2)), C(z_(3)) are the vertices of an equilateral triangle ABC, then arg (2z_(1)-z_(2)-z_(3))/(z_(3)_z_(2))=

If z_(1)z_(2),z_(3) and z_(4) taken in order vertices of a rhombus, then proves that Re((z_(3)-z_(1))/(z_(4)-z_(2))) = 0

If z_(1), z_(2), z_(3), z_(4) are complex numbers, show that they are vertices of a parallelogram In the Argand diagram if and only if z_(1) + z_(3)= z_(2) + z_(4)

If |z_(1)|=|z_(2)| and arg (z_(1))+"arg"(z_(2))=0 , then

If z_(1)=1+2i, z_(2)=2+3i, z_(3)=3+4i , then z_(1),z_(2) and z_(3) represent the vertices of a/an.