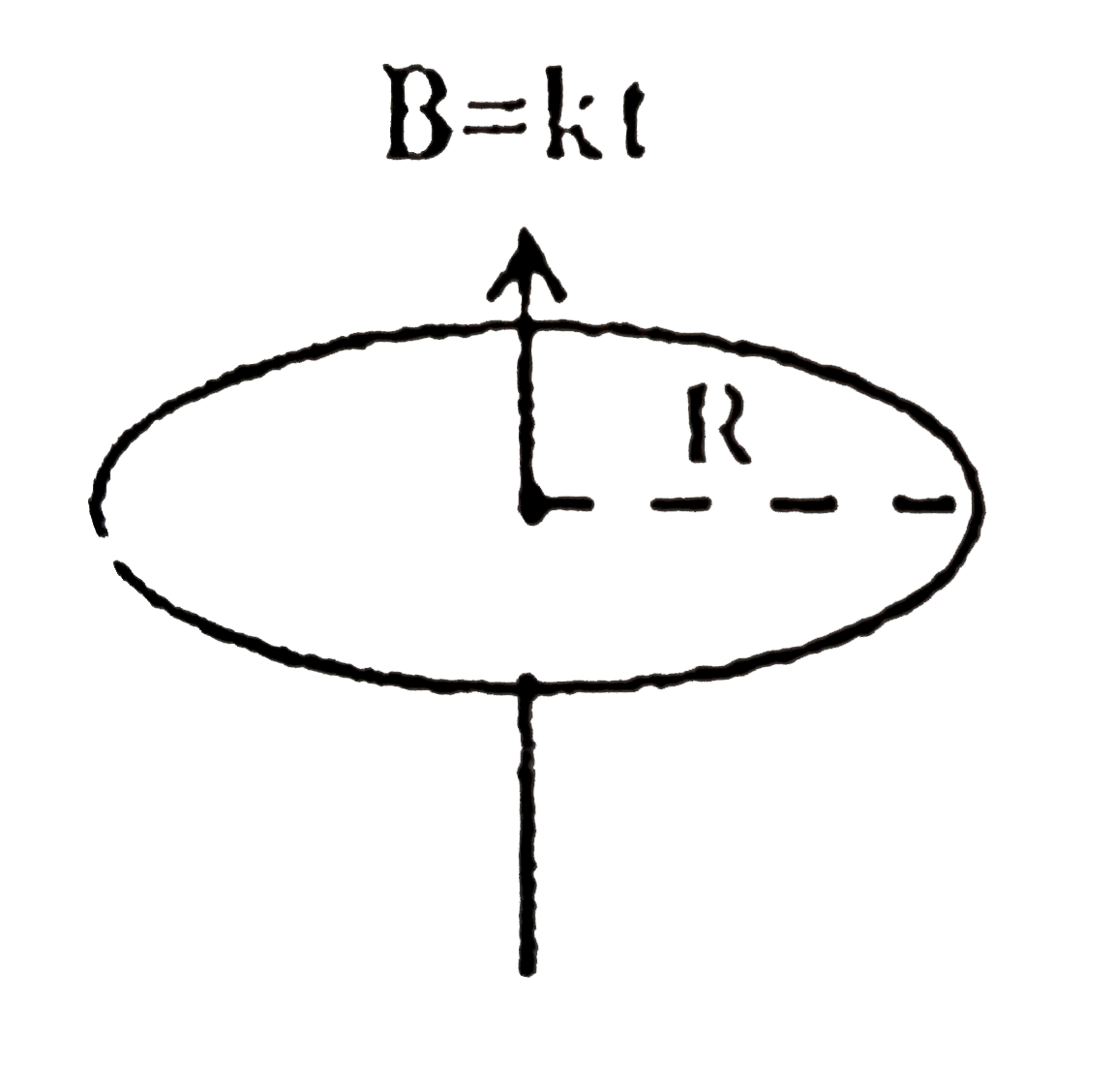
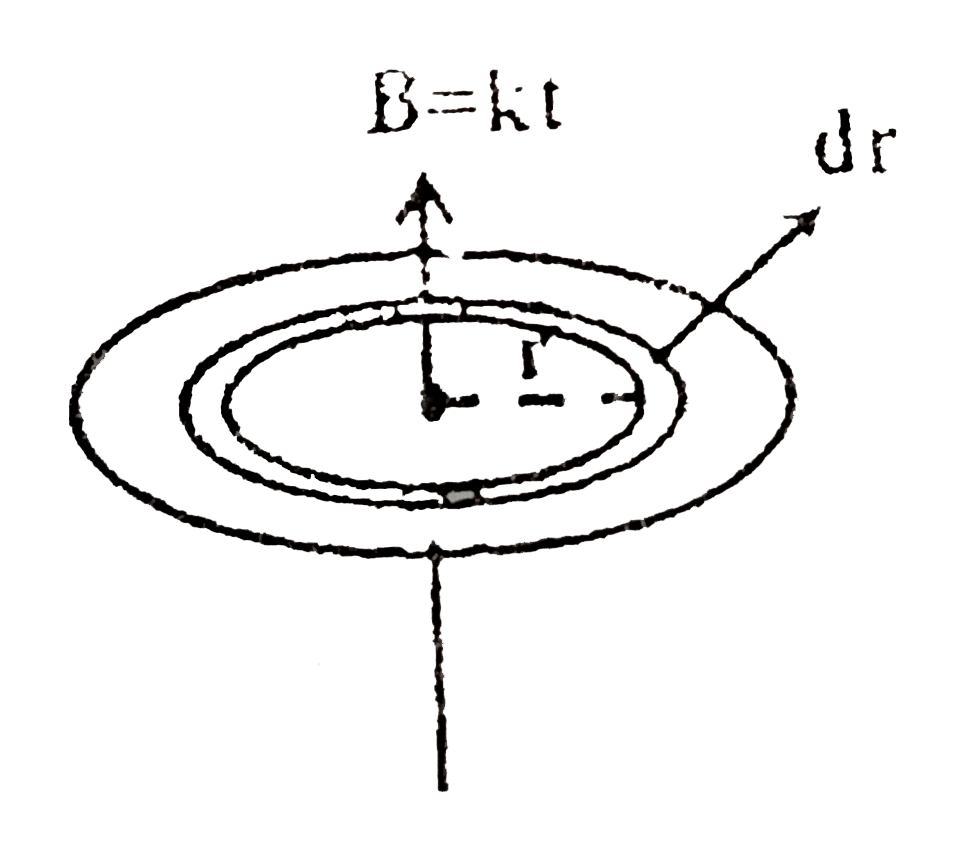
Text Solution
Verified by Experts
Recommended Questions
- A thin non conducting horizontal disc of mass m having total charge q ...
Text Solution
|
- A charge q is uniformly distributed on a non-conducting disc of radius...
Text Solution
|
- A non-conducting thin disc of radius R charged uniformly over one side...
Text Solution
|
- A non-conducting thin disc of radius R charged uniformly over one side...
Text Solution
|
- A non-conducting thin disc of radius R and mass m having charge unifor...
Text Solution
|
- A non conducting disc of radius R, charge q is rotating about an axis ...
Text Solution
|
- Charge Q is uniformly distributed on the rim of a thin insulating disc...
Text Solution
|
- A disc of mass m has a charge Q distributed on its surface. It is rota...
Text Solution
|
- A flat disc of radius R charged uniformly on its surface at a surface ...
Text Solution
|