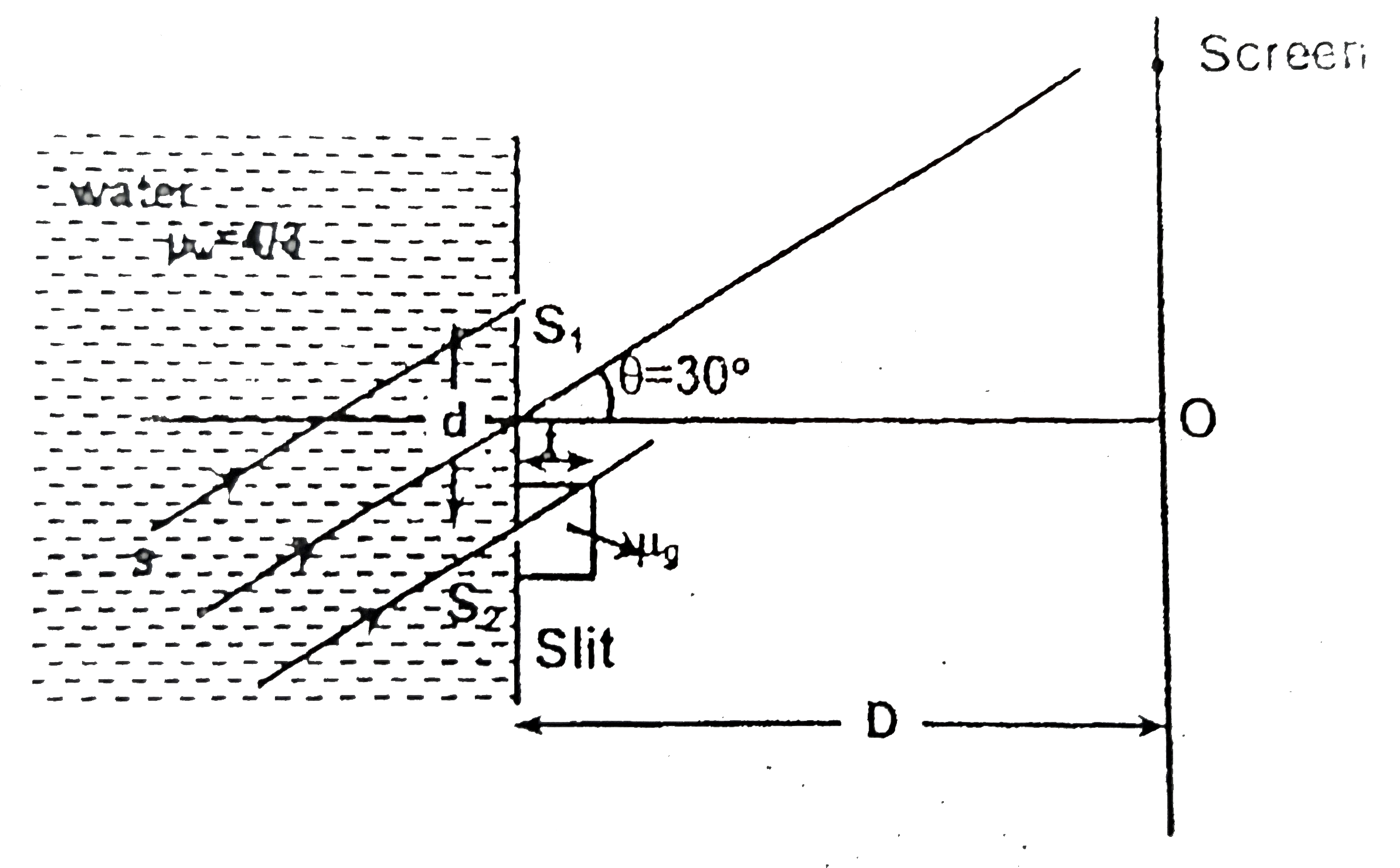
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- In a YDSE experiment the two slits are covered with a transparent memb...
Text Solution
|
- A YDSE is performed in a medium of refractive index 4 // 3 , A light o...
Text Solution
|
- Young's double-slit experiment setup with ligth of wavelength lambda =...
Text Solution
|
- Young's double-slit experiment setup with ligth of wavelength lambda =...
Text Solution
|
- In YSDE, both slits are covered by transparent slab. Upper slit is cov...
Text Solution
|
- एक double slit उपकरण में एक स्लिट पर 0.02 mm मोटाई का एक पारदर्शी पन्न...
Text Solution
|
- In biprism experiment the fringe width is 0.30 mm . If slits are cover...
Text Solution
|
- यंग के द्विस्लिट प्रयोग में स्लिटों के बीच की दुरी 2 मिमी, स्लिटों से ...
Text Solution
|
- In a Young's d ouble slit experiment, a monochromatic light of wavel...
Text Solution
|