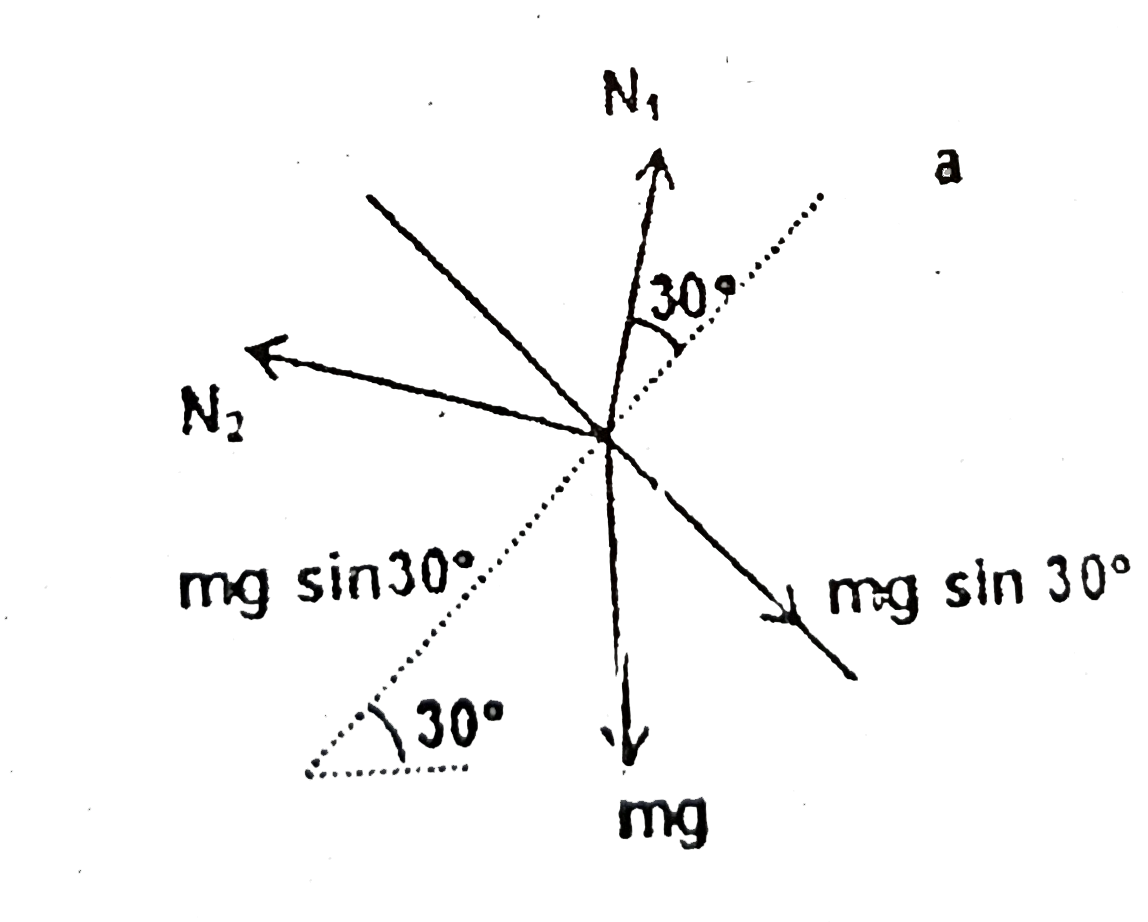
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A cylinder of mass m rests on a supporting block as shown. If beta=60^...
Text Solution
|
- A cylinder of mass m and radius R rolls down an inclined plane of incl...
Text Solution
|
- A block of mass m is placed at rest on an inclination theta to the hor...
Text Solution
|
- A cylinder of mass m and radius R rolls down an inclined plane of incl...
Text Solution
|
- A system consists of block A and B each of mass m connected by a light...
Text Solution
|
- A system consists of block A and B each of mass m connected by a light...
Text Solution
|
- In the arrangement shown in the figure, block A of mass 8 kg rests on ...
Text Solution
|
- In the arrangement shown in figure the cylinder of mass M is at rest o...
Text Solution
|
- The axis of the uniform cylinder in figure is fixed. The cylinder is i...
Text Solution
|