Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
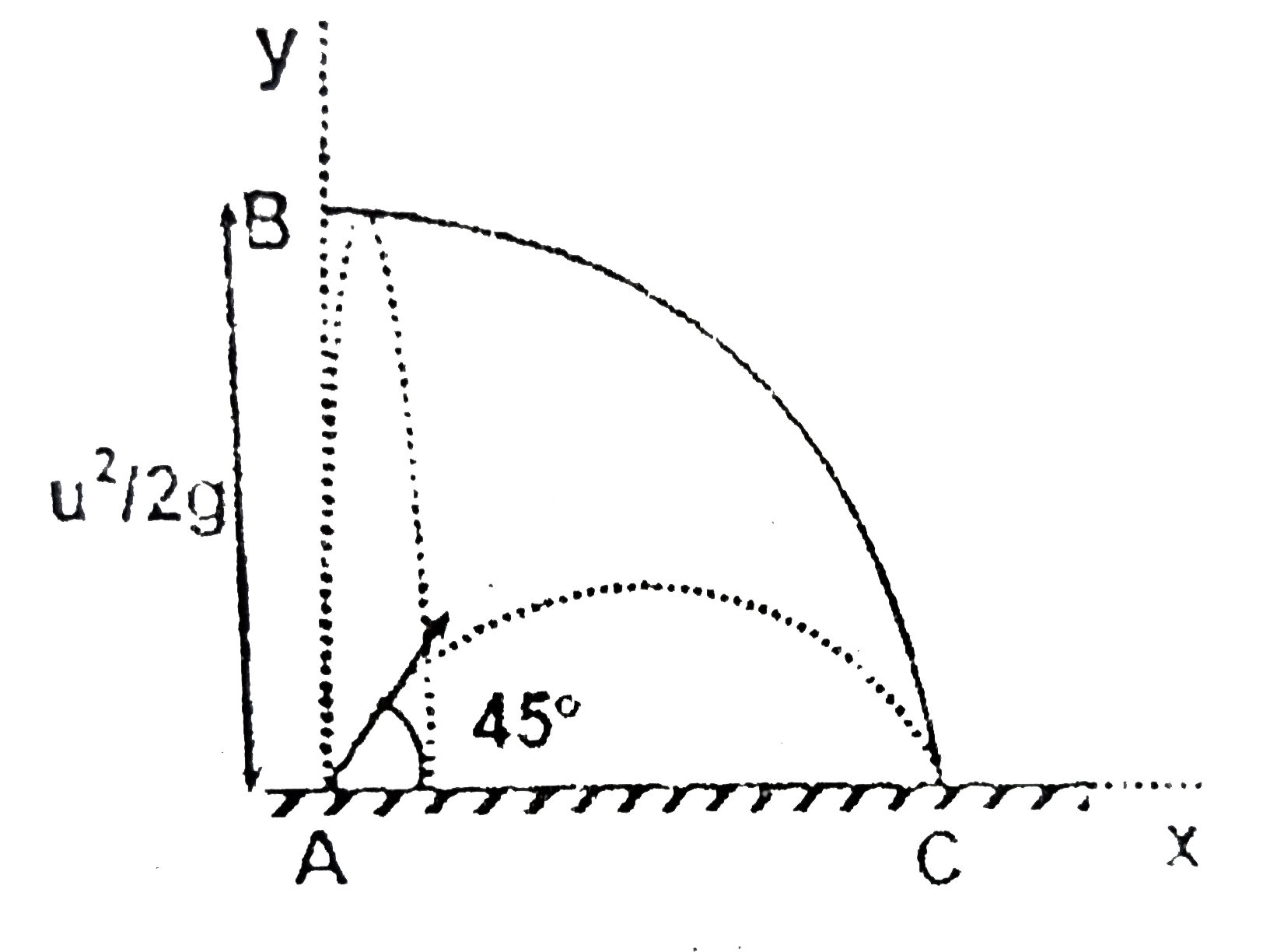
- A particle P is to be projected from a fixed point A on the ground wit...
Text Solution
|
- Figure shows that particle A is projected from point P with velocity u...
Text Solution
|
- A particle is projected with speed u at angle theta to the horizontal....
Text Solution
|
- Two particles A and B are projected simultaneously from a fixed point ...
Text Solution
|
- A particle is projected from ground at an angle theta with horizontal ...
Text Solution
|
- A particle is projected from the ground with an initial speed of u at ...
Text Solution
|
- A particle is projected at an angle theta with the horizontal . If ang...
Text Solution
|
- A particle is projected fro the ground with an initial speed v at an a...
Text Solution
|
- A particle is projected from the ground with an initial speed v at an ...
Text Solution
|