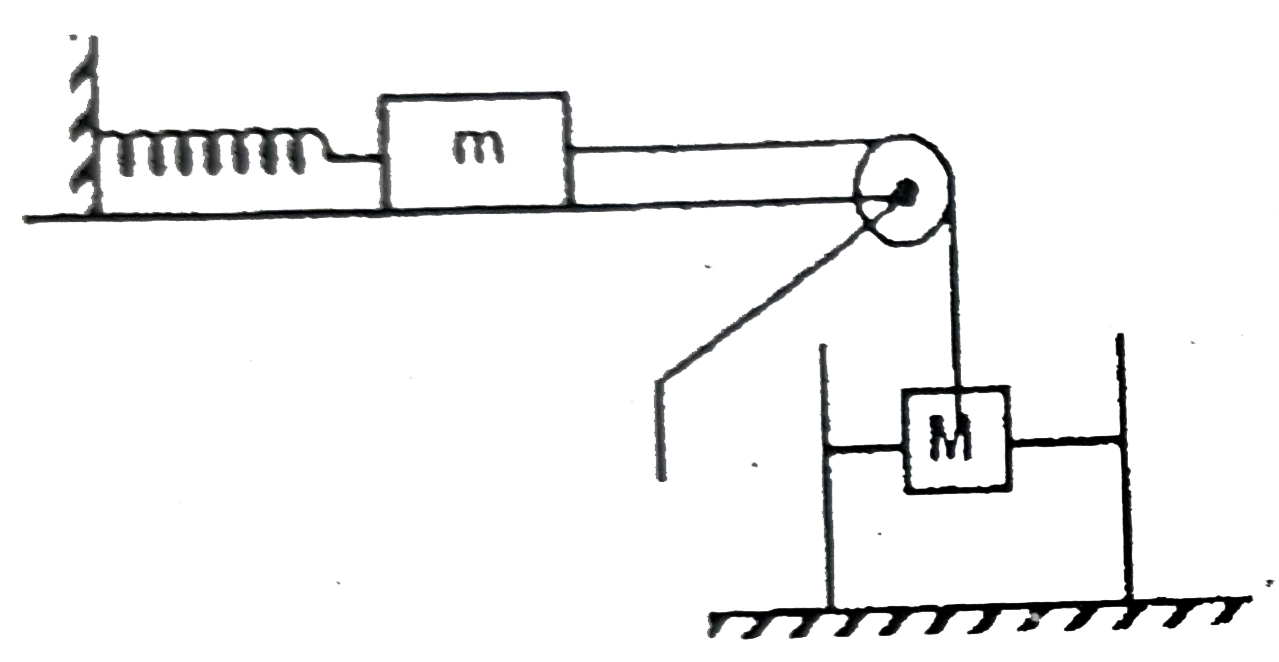
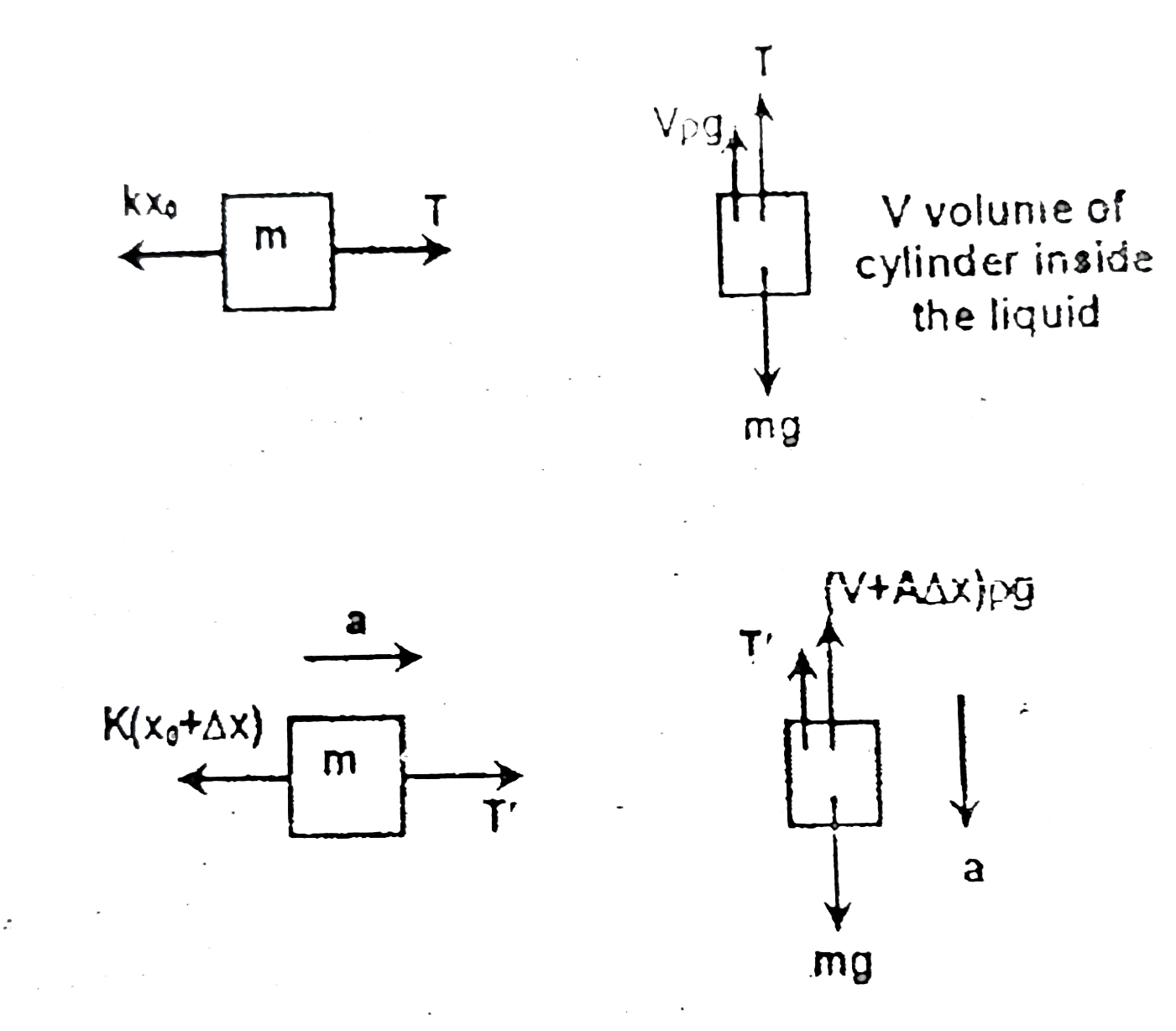
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- For the arrangement shown, a cylinder of mass m with cross-sectional a...
Text Solution
|
- A plank of mass 'm' and area of cross - section A is floating in a non...
Text Solution
|
- The acceleration displacement graph of a particle executing simple har...
Text Solution
|
- A rectangular block of mass m and area of cross-section A floats in a ...
Text Solution
|
- A block of rectangular size of mass m and area of cross section A, flo...
Text Solution
|
- A solid cylinder of denisty rho(0) , cross-section area A and length l...
Text Solution
|
- A rectangular block of mass m and area of cross-section A floats in a ...
Text Solution
|
- A piece of wood of mass m is floating erect in a liquid whose density ...
Text Solution
|
- A rectangular block of mass m and area of cross-section A floats in a ...
Text Solution
|